
Question Number 114167 by mohammad17 last updated on 17/Sep/20
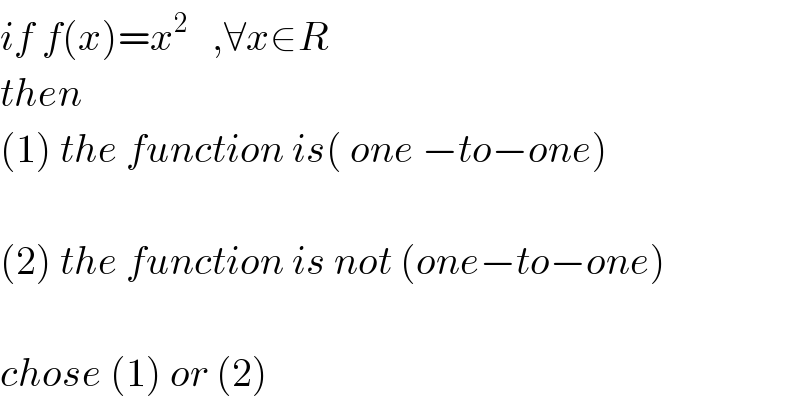
$${if}\:{f}\left({x}\right)={x}^{\mathrm{2}} \:\:\:,\forall{x}\in{R} \\ $$$${then}\: \\ $$$$\left(\mathrm{1}\right)\:{the}\:{function}\:{is}\left(\:{one}\:−{to}−{one}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:{the}\:{function}\:{is}\:{not}\:\left({one}−{to}−{one}\right) \\ $$$$ \\ $$$${chose}\:\left(\mathrm{1}\right)\:{or}\:\left(\mathrm{2}\right) \\ $$
Commented by mohammad17 last updated on 17/Sep/20

$${help}\:{me}\:{sir} \\ $$
Commented by bobhans last updated on 17/Sep/20
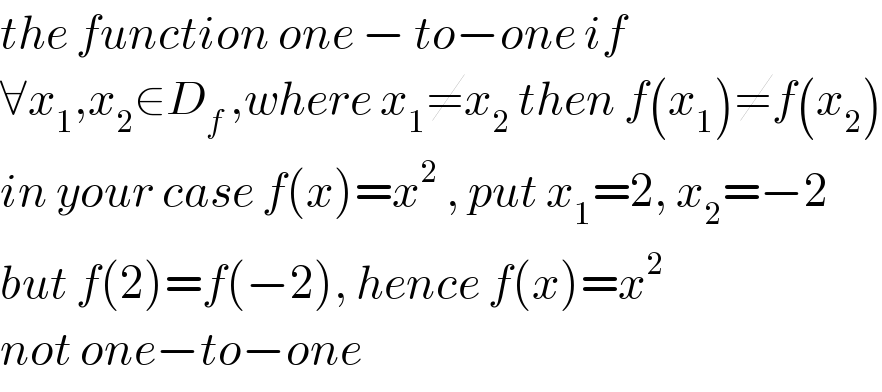
$${the}\:{function}\:{one}\:−\:{to}−{one}\:{if}\: \\ $$$$\forall{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} \in{D}_{{f}} \:,{where}\:{x}_{\mathrm{1}} \neq{x}_{\mathrm{2}} \:{then}\:{f}\left({x}_{\mathrm{1}} \right)\neq{f}\left({x}_{\mathrm{2}} \right) \\ $$$${in}\:{your}\:{case}\:{f}\left({x}\right)={x}^{\mathrm{2}} \:,\:{put}\:{x}_{\mathrm{1}} =\mathrm{2},\:{x}_{\mathrm{2}} =−\mathrm{2} \\ $$$${but}\:{f}\left(\mathrm{2}\right)={f}\left(−\mathrm{2}\right),\:{hence}\:{f}\left({x}\right)={x}^{\mathrm{2}} \\ $$$${not}\:{one}−{to}−{one} \\ $$
