
Question Number 114146 by Eric002 last updated on 17/Sep/20
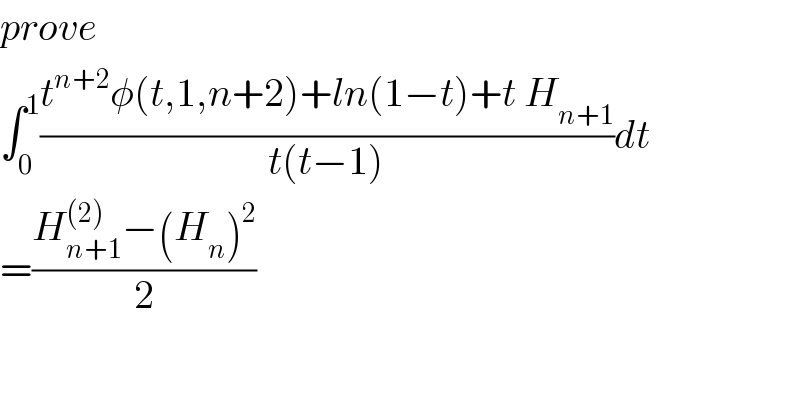
$${prove} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{n}+\mathrm{2}} \phi\left({t},\mathrm{1},{n}+\mathrm{2}\right)+{ln}\left(\mathrm{1}−{t}\right)+{t}\:{H}_{{n}+\mathrm{1}} }{{t}\left({t}−\mathrm{1}\right)}{dt} \\ $$$$=\frac{{H}_{{n}+\mathrm{1}} ^{\left(\mathrm{2}\right)} −\left({H}_{{n}} \right)^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by mindispower last updated on 18/Sep/20
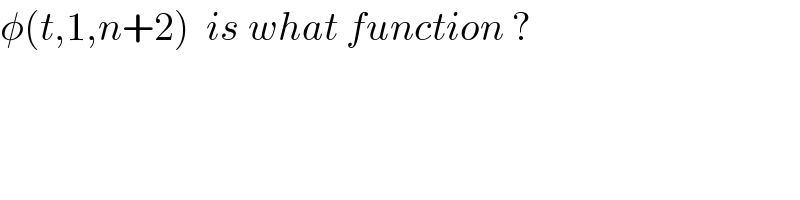
$$\phi\left({t},\mathrm{1},{n}+\mathrm{2}\right)\:\:{is}\:{what}\:{function}\:? \\ $$
Commented by Eric002 last updated on 18/Sep/20
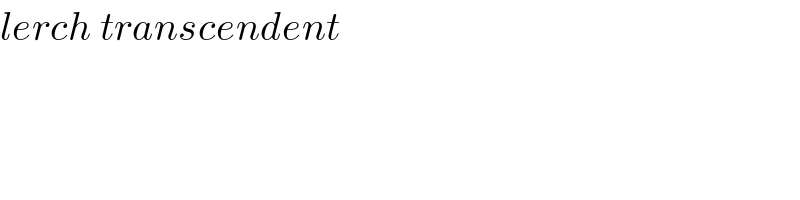
$${lerch}\:{transcendent}\: \\ $$
