
Question Number 114075 by bemath last updated on 17/Sep/20
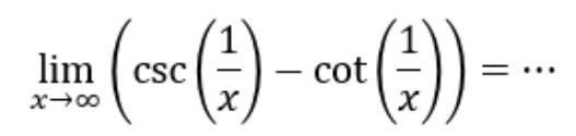
Answered by john santu last updated on 17/Sep/20
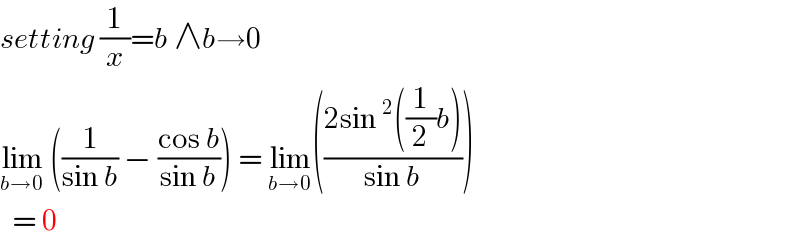
$${setting}\:\frac{\mathrm{1}}{{x}}={b}\:\wedge{b}\rightarrow\mathrm{0} \\ $$$$\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{sin}\:{b}}\:−\:\frac{\mathrm{cos}\:{b}}{\mathrm{sin}\:{b}}\right)\:=\:\underset{{b}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}{b}\right)}{\mathrm{sin}\:{b}}\right) \\ $$$$\:\:=\:\mathrm{0} \\ $$
Answered by Olaf last updated on 17/Sep/20
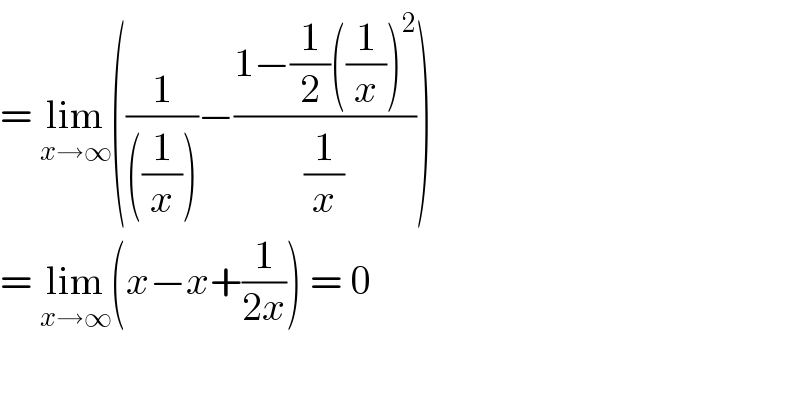
$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{x}}\right)}−\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{\frac{\mathrm{1}}{{x}}}\right) \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}−{x}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$
