
Question Number 114066 by john santu last updated on 17/Sep/20
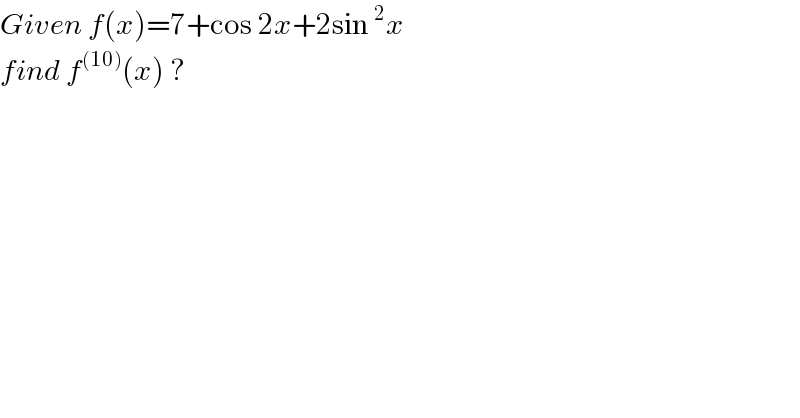
$${Given}\:{f}\left({x}\right)=\mathrm{7}+\mathrm{cos}\:\mathrm{2}{x}+\mathrm{2sin}\:^{\mathrm{2}} {x} \\ $$$${find}\:{f}^{\left(\mathrm{10}\right)} \left({x}\right)\:? \\ $$
Commented by bemath last updated on 17/Sep/20
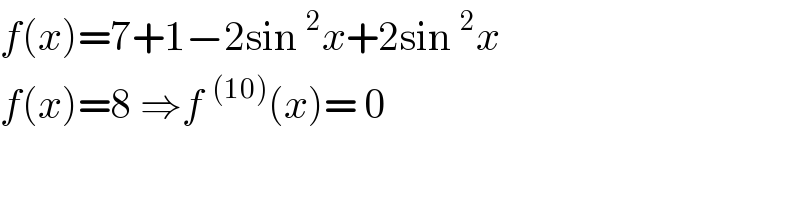
$${f}\left({x}\right)=\mathrm{7}+\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}+\mathrm{2sin}\:^{\mathrm{2}} {x} \\ $$$${f}\left({x}\right)=\mathrm{8}\:\Rightarrow{f}\:^{\left(\mathrm{10}\right)} \left({x}\right)=\:\mathrm{0}\: \\ $$
Answered by Olaf last updated on 17/Sep/20
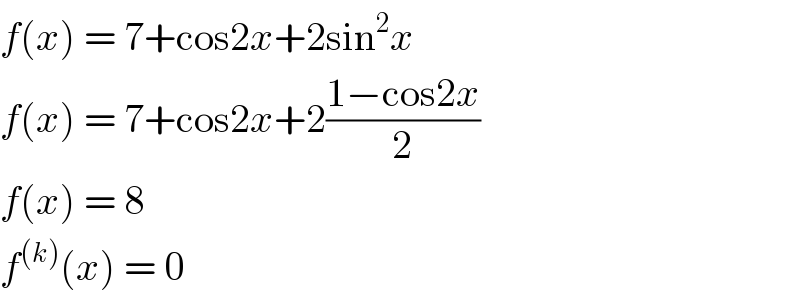
$${f}\left({x}\right)\:=\:\mathrm{7}+\mathrm{cos2}{x}+\mathrm{2sin}^{\mathrm{2}} {x} \\ $$$${f}\left({x}\right)\:=\:\mathrm{7}+\mathrm{cos2}{x}+\mathrm{2}\frac{\mathrm{1}−\mathrm{cos2}{x}}{\mathrm{2}} \\ $$$${f}\left({x}\right)\:=\:\mathrm{8} \\ $$$${f}^{\left({k}\right)} \left({x}\right)\:=\:\mathrm{0} \\ $$
Answered by 1549442205PVT last updated on 17/Sep/20
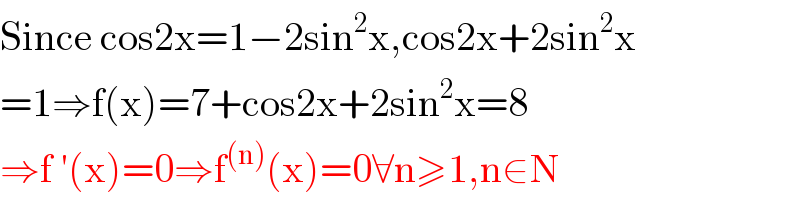
$$\mathrm{Since}\:\mathrm{cos2x}=\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \mathrm{x},\mathrm{cos2x}+\mathrm{2sin}^{\mathrm{2}} \mathrm{x} \\ $$$$=\mathrm{1}\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{7}+\mathrm{cos2x}+\mathrm{2sin}^{\mathrm{2}} \mathrm{x}=\mathrm{8} \\ $$$$\Rightarrow\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{0}\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)=\mathrm{0}\forall\mathrm{n}\geqslant\mathrm{1},\mathrm{n}\in\mathrm{N} \\ $$
