
Question Number 113959 by mohammad17 last updated on 16/Sep/20
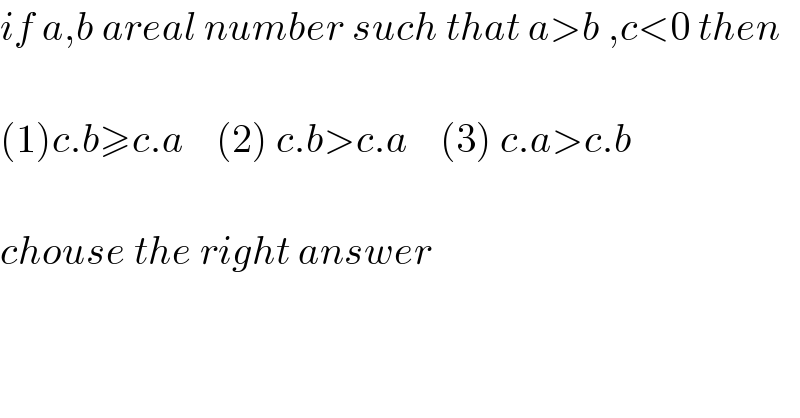
$${if}\:{a},{b}\:{areal}\:{number}\:{such}\:{that}\:{a}>{b}\:,{c}<\mathrm{0}\:{then}\: \\ $$ $$ \\ $$ $$\left(\mathrm{1}\right){c}.{b}\geqslant{c}.{a}\:\:\:\:\left(\mathrm{2}\right)\:{c}.{b}>{c}.{a}\:\:\:\:\left(\mathrm{3}\right)\:{c}.{a}>{c}.{b} \\ $$ $$ \\ $$ $${chouse}\:{the}\:{right}\:{answer} \\ $$
Answered by 1549442205PVT last updated on 16/Sep/20

$$\mathrm{Choose}\:\left(\mathrm{2}\right)\:\:\mathrm{because}\:\mathrm{from}\:\mathrm{a}>\mathrm{b}\:\mathrm{multiplying} \\ $$ $$\mathrm{two}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{by}\:\mathrm{one} \\ $$ $$\mathrm{number}\:\mathrm{c}<\mathrm{0}\:\mathrm{we}\:\mathrm{will}\:\mathrm{obtain}\:\mathrm{an} \\ $$ $$\mathrm{inequality}\:\mathrm{with}\:\mathrm{opposite}\:\:\mathrm{sign} \\ $$ $$\mathrm{ac}<\mathrm{bc}\:\mathrm{or}\:\mathrm{cb}>\mathrm{ca} \\ $$
