
Question Number 11395 by Joel576 last updated on 23/Mar/17
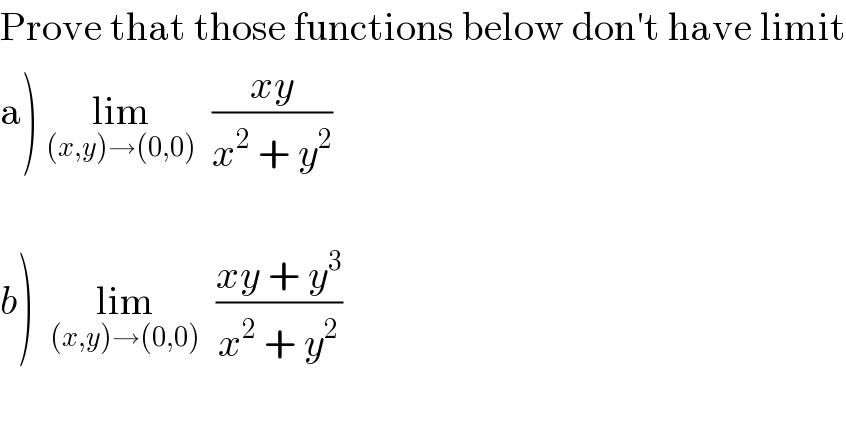
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{those}\:\mathrm{functions}\:\mathrm{below}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{limit} \\ $$$$\left.\mathrm{a}\right)\:\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\:\frac{{xy}}{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} } \\ $$$$ \\ $$$$\left.{b}\right)\:\:\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\:\frac{{xy}\:+\:{y}^{\mathrm{3}} }{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} } \\ $$
Commented by prakash jain last updated on 23/Mar/17
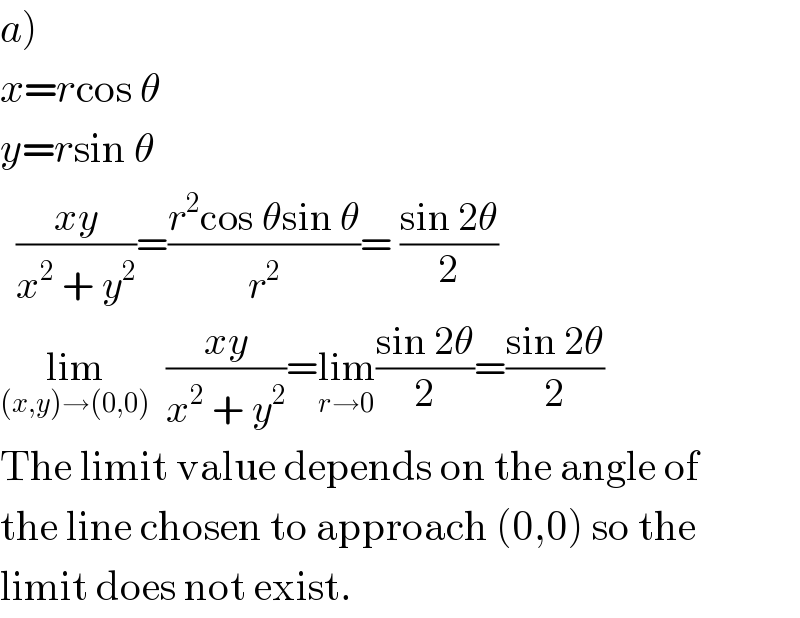
$$\left.{a}\right) \\ $$$${x}={r}\mathrm{cos}\:\theta \\ $$$${y}={r}\mathrm{sin}\:\theta \\ $$$$\:\:\frac{{xy}}{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} }=\frac{{r}^{\mathrm{2}} \mathrm{cos}\:\theta\mathrm{sin}\:\theta}{{r}^{\mathrm{2}} }=\:\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:\:\frac{{xy}}{{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} }=\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}=\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{limit}\:\mathrm{value}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{line}\:\mathrm{chosen}\:\mathrm{to}\:\mathrm{approach}\:\left(\mathrm{0},\mathrm{0}\right)\:\mathrm{so}\:\mathrm{the} \\ $$$$\mathrm{limit}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist}. \\ $$
