
Question Number 113897 by Lordose last updated on 16/Sep/20
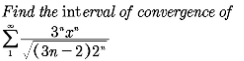
Answered by mathmax by abdo last updated on 17/Sep/20
![let u_n =(3^n /(√((3n−2)2^n ))) ⇒u_n =((((3/(√2)))^n )/(√(3n−2))) (n≥1) ⇒ (u_(n+1) /u_n ) =((((3/(√2)))^(n+1) )/(√(3n+1)))×((√(3n−2))/(((3/(√2)))^n )) =(√((3n−2)/(3n+1)))×((3/(√2))) and lim_(n→+∞) (u_(n+1) /u_n ) =(3/(√2)) so for ∣x∣ <(3/(√2)) the serie converges and for ∣x∣≥(3/(√2)) the serie diverges finally I_c =]−(3/(√2)),(3/(√2))[](Q114059.png)
$$\mathrm{let}\:\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{3}^{\mathrm{n}} }{\sqrt{\left(\mathrm{3n}−\mathrm{2}\right)\mathrm{2}^{\mathrm{n}} }}\:\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{n}} }{\sqrt{\mathrm{3n}−\mathrm{2}}}\:\:\left(\mathrm{n}\geqslant\mathrm{1}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }\:=\frac{\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{n}+\mathrm{1}} }{\sqrt{\mathrm{3n}+\mathrm{1}}}×\frac{\sqrt{\mathrm{3n}−\mathrm{2}}}{\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{n}} }\:=\sqrt{\frac{\mathrm{3n}−\mathrm{2}}{\mathrm{3n}+\mathrm{1}}}×\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\right)\:\:\mathrm{and}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} } \\ $$$$=\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\:\:\mathrm{so}\:\mathrm{for}\:\mid\mathrm{x}\mid\:<\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\:\:\mathrm{the}\:\mathrm{serie}\:\mathrm{converges}\:\mathrm{and}\:\mathrm{for}\:\mid\mathrm{x}\mid\geqslant\frac{\mathrm{3}}{\sqrt{\mathrm{2}}} \\ $$$$\left.\mathrm{the}\:\mathrm{serie}\:\mathrm{diverges}\:\mathrm{finally}\:\mathrm{I}_{\mathrm{c}} =\right]−\frac{\mathrm{3}}{\sqrt{\mathrm{2}}},\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\left[\right. \\ $$
