
Question Number 113824 by deepraj123 last updated on 15/Sep/20
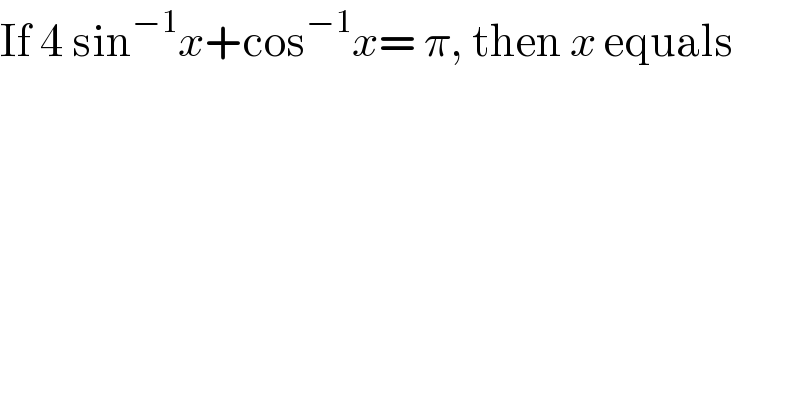
$$\mathrm{If}\:\mathrm{4}\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{cos}^{−\mathrm{1}} {x}=\:\pi,\:\mathrm{then}\:{x}\:\mathrm{equals} \\ $$
Answered by $@y@m last updated on 15/Sep/20
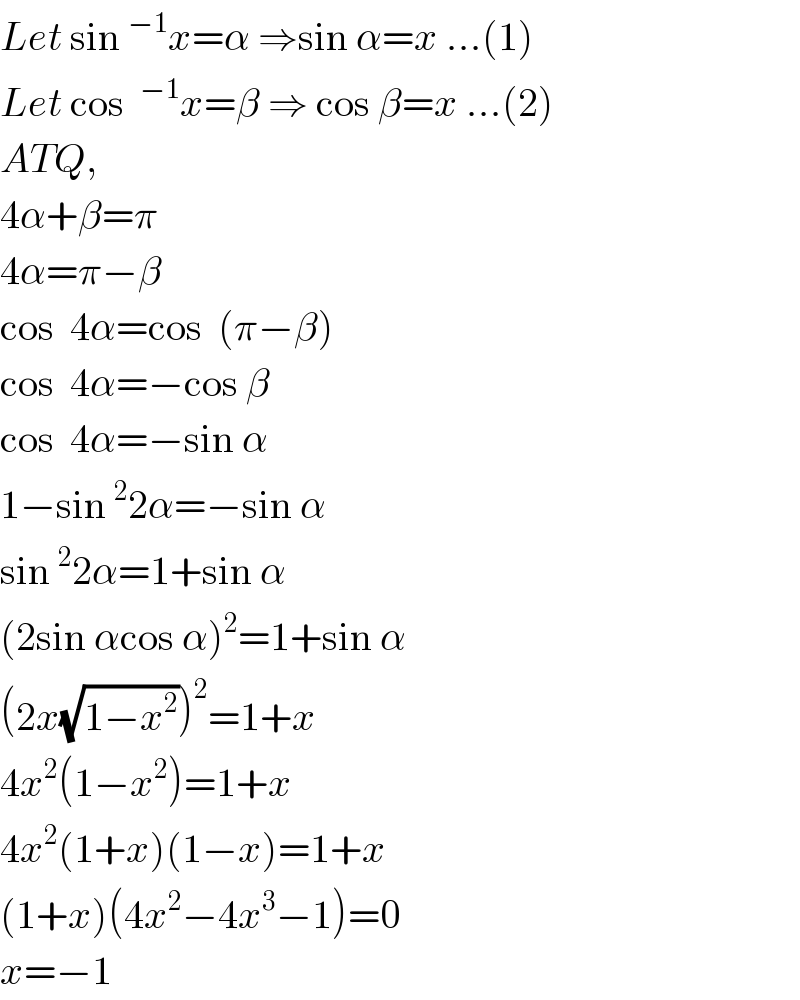
$${Let}\:\mathrm{sin}\:^{−\mathrm{1}} {x}=\alpha\:\Rightarrow\mathrm{sin}\:\alpha={x}\:...\left(\mathrm{1}\right) \\ $$$${Let}\:\mathrm{cos}\:\:^{−\mathrm{1}} {x}=\beta\:\Rightarrow\:\mathrm{cos}\:\beta={x}\:...\left(\mathrm{2}\right) \\ $$$${ATQ}, \\ $$$$\mathrm{4}\alpha+\beta=\pi \\ $$$$\mathrm{4}\alpha=\pi−\beta \\ $$$$\mathrm{cos}\:\:\mathrm{4}\alpha=\mathrm{cos}\:\:\left(\pi−\beta\right) \\ $$$$\mathrm{cos}\:\:\mathrm{4}\alpha=−\mathrm{cos}\:\beta \\ $$$$\mathrm{cos}\:\:\mathrm{4}\alpha=−\mathrm{sin}\:\alpha \\ $$$$\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\alpha=−\mathrm{sin}\:\alpha \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\alpha=\mathrm{1}+\mathrm{sin}\:\alpha \\ $$$$\left(\mathrm{2sin}\:\alpha\mathrm{cos}\:\alpha\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{sin}\:\alpha \\ $$$$\left(\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{1}+{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\mathrm{1}+{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)=\mathrm{1}+{x} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1} \\ $$
