
Question Number 113742 by bemath last updated on 15/Sep/20
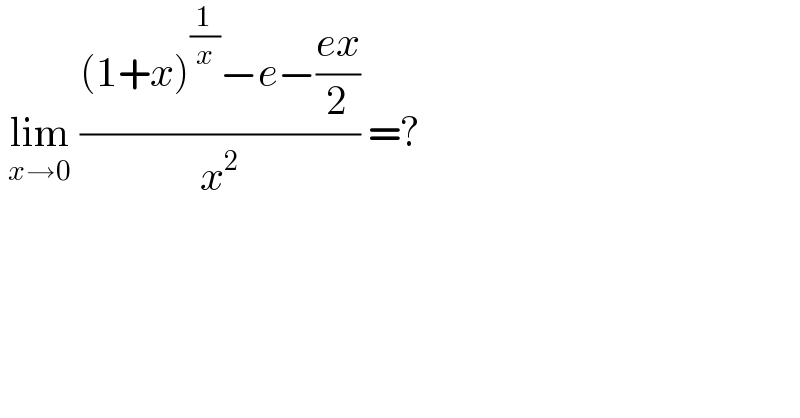
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} −{e}−\frac{{ex}}{\mathrm{2}}}{{x}^{\mathrm{2}} }\:=?\: \\ $$
Answered by bobhans last updated on 15/Sep/20
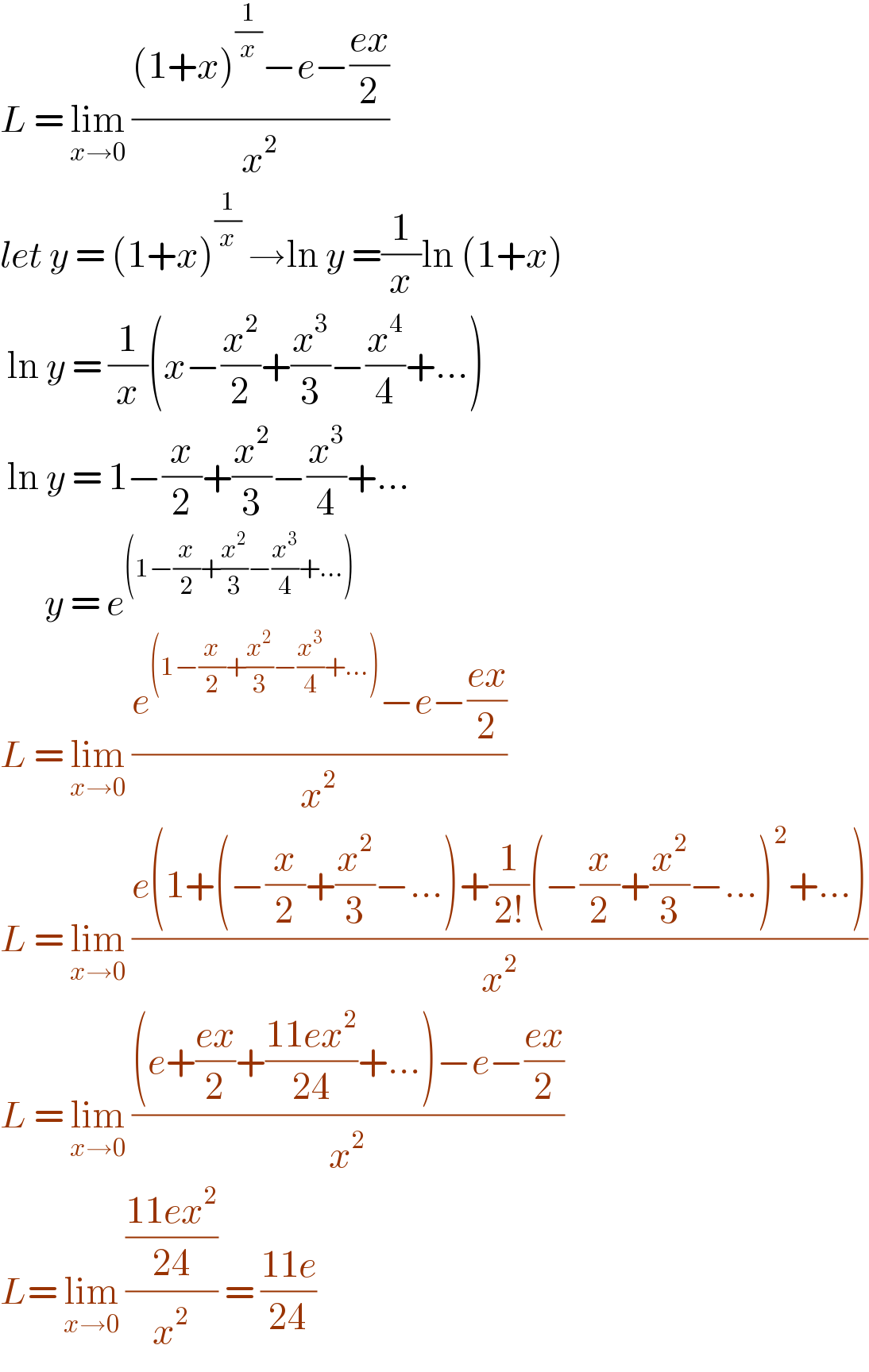
$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} −{e}−\frac{{ex}}{\mathrm{2}}}{{x}^{\mathrm{2}} }\: \\ $$$${let}\:{y}\:=\:\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} \:\rightarrow\mathrm{ln}\:{y}\:=\frac{\mathrm{1}}{{x}}\mathrm{ln}\:\left(\mathrm{1}+{x}\right) \\ $$$$\:\mathrm{ln}\:{y}\:=\:\frac{\mathrm{1}}{{x}}\left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+...\right) \\ $$$$\:\mathrm{ln}\:{y}\:=\:\mathrm{1}−\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+... \\ $$$$\:\:\:\:\:\:\:{y}\:=\:{e}^{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+...\right)} \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+...\right)} −{e}−\frac{{ex}}{\mathrm{2}}}{{x}^{\mathrm{2}} } \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}\left(\mathrm{1}+\left(−\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−...\right)+\frac{\mathrm{1}}{\mathrm{2}!}\left(−\frac{{x}}{\mathrm{2}}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−...\right)^{\mathrm{2}} +...\right)}{{x}^{\mathrm{2}} } \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({e}+\frac{{ex}}{\mathrm{2}}+\frac{\mathrm{11}{ex}^{\mathrm{2}} }{\mathrm{24}}+...\right)−{e}−\frac{{ex}}{\mathrm{2}}}{{x}^{\mathrm{2}} } \\ $$$${L}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{11}{ex}^{\mathrm{2}} }{\mathrm{24}}}{{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{11}{e}}{\mathrm{24}} \\ $$
Answered by mathmax by abdo last updated on 16/Sep/20

$$\mathrm{let}\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{e}−\frac{\mathrm{ex}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)} −\mathrm{e}−\frac{\mathrm{ex}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\mathrm{1}−\mathrm{x}\:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)\:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\:=\mathrm{1}−\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)} \:=\mathrm{e}\:\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)} \:\sim\mathrm{e}\:\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)\:=\mathrm{e}−\frac{\mathrm{ex}}{\mathrm{2}}+\frac{\mathrm{ex}^{\mathrm{2}} }{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)} −\mathrm{e}+\frac{\mathrm{ex}}{\mathrm{2}}\:\sim\:\frac{\mathrm{ex}^{\mathrm{2}} }{\mathrm{3}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\sim\frac{\mathrm{e}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{e}}{\mathrm{3}} \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{e}+\frac{\mathrm{ex}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} }\:...! \\ $$
