
Question Number 113641 by ZiYangLee last updated on 14/Sep/20
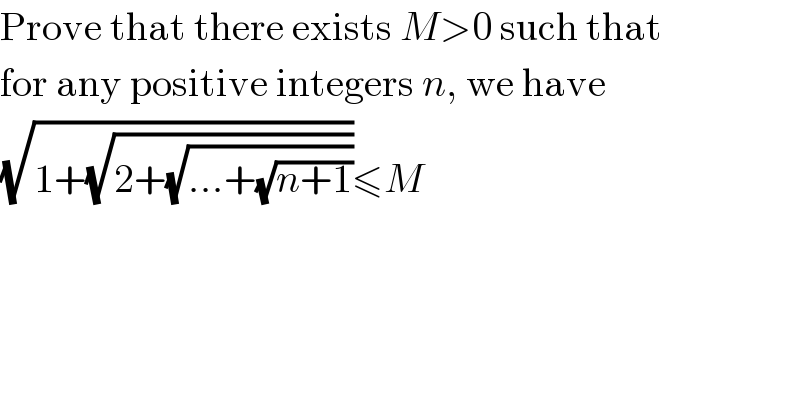
$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{there}\:\mathrm{exists}\:{M}>\mathrm{0}\:\mathrm{such}\:\mathrm{that} \\ $$ $$\mathrm{for}\:\mathrm{any}\:\mathrm{positive}\:\mathrm{integers}\:{n},\:\mathrm{we}\:\mathrm{have} \\ $$ $$\sqrt{\mathrm{1}+\sqrt{\mathrm{2}+\sqrt{...+\sqrt{{n}+\mathrm{1}}}}}\leqslant{M} \\ $$
Commented bymr W last updated on 14/Sep/20
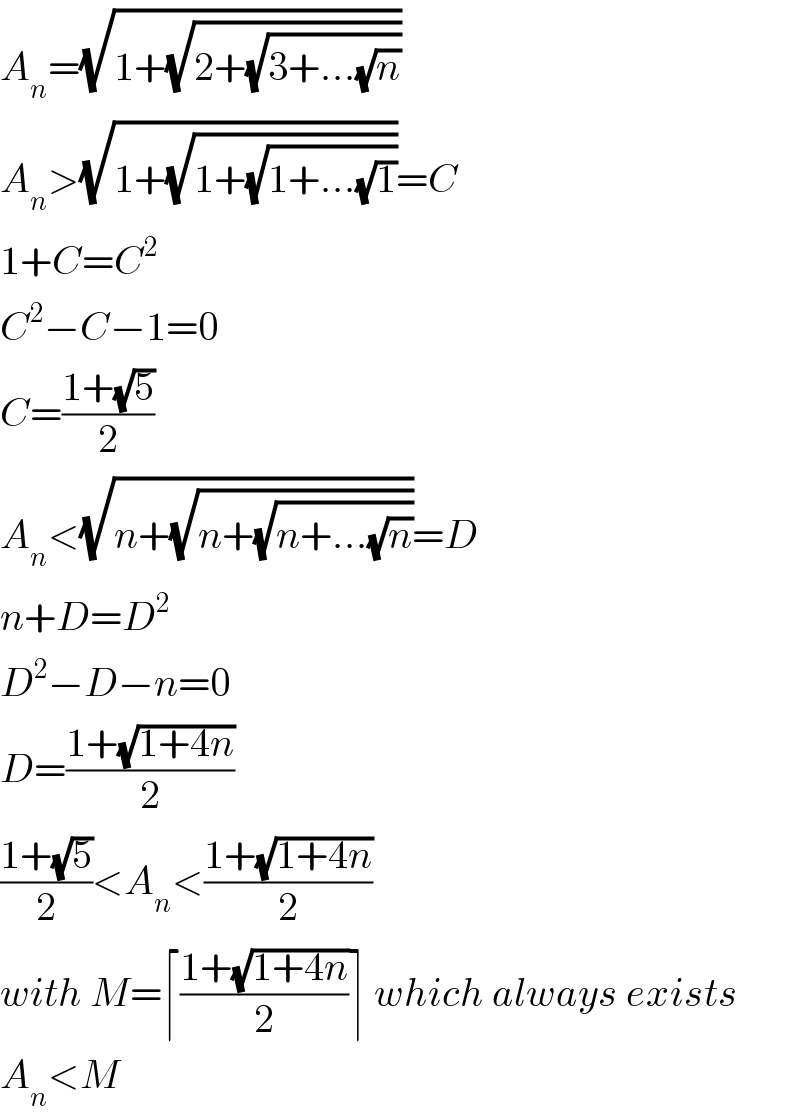
$${A}_{{n}} =\sqrt{\mathrm{1}+\sqrt{\mathrm{2}+\sqrt{\mathrm{3}+...\sqrt{{n}}}}} \\ $$ $${A}_{{n}} >\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+...\sqrt{\mathrm{1}}}}}={C} \\ $$ $$\mathrm{1}+{C}={C}^{\mathrm{2}} \\ $$ $${C}^{\mathrm{2}} −{C}−\mathrm{1}=\mathrm{0} \\ $$ $${C}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$ $${A}_{{n}} <\sqrt{{n}+\sqrt{{n}+\sqrt{{n}+...\sqrt{{n}}}}}={D} \\ $$ $${n}+{D}={D}^{\mathrm{2}} \\ $$ $${D}^{\mathrm{2}} −{D}−{n}=\mathrm{0} \\ $$ $${D}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{n}}}{\mathrm{2}} \\ $$ $$\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}<{A}_{{n}} <\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{n}}}{\mathrm{2}} \\ $$ $${with}\:{M}=\lceil\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{n}}}{\mathrm{2}}\rceil\:{which}\:{always}\:{exists} \\ $$ $${A}_{{n}} <{M} \\ $$
