
Question Number 11364 by Joel576 last updated on 22/Mar/17
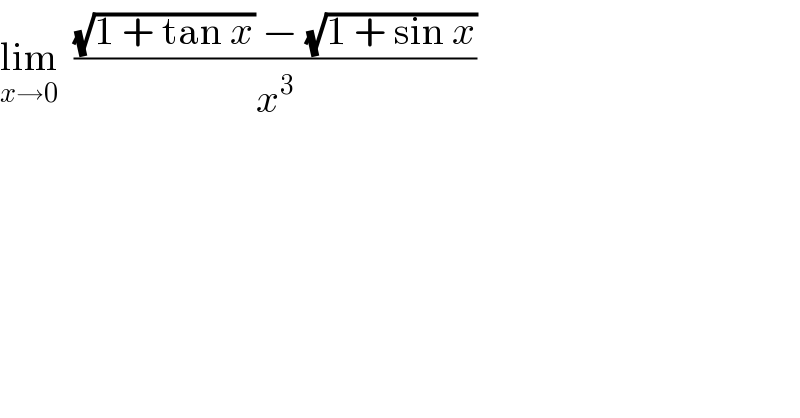
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\sqrt{\mathrm{1}\:+\:\mathrm{tan}\:{x}}\:−\:\sqrt{\mathrm{1}\:+\:\mathrm{sin}\:{x}}}{{x}^{\mathrm{3}} } \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Mar/17
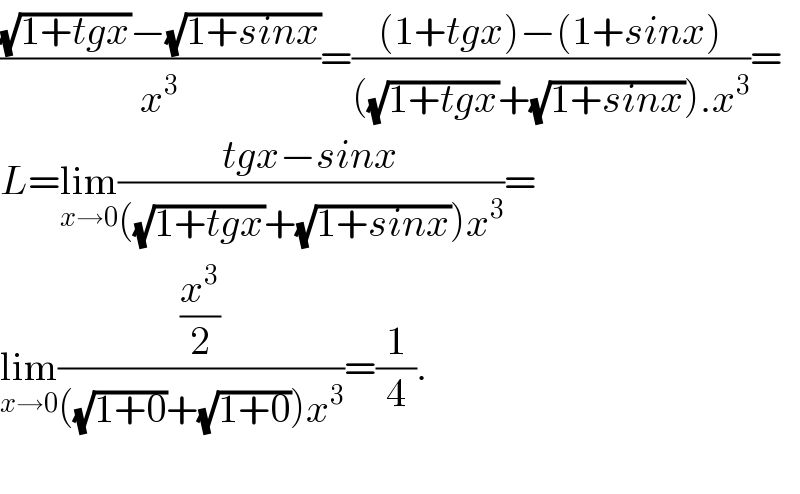
$$\frac{\sqrt{\mathrm{1}+{tgx}}−\sqrt{\mathrm{1}+{sinx}}}{{x}^{\mathrm{3}} }=\frac{\left(\mathrm{1}+{tgx}\right)−\left(\mathrm{1}+{sinx}\right)}{\left(\sqrt{\mathrm{1}+{tgx}}+\sqrt{\mathrm{1}+{sinx}}\right).{x}^{\mathrm{3}} }= \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{tgx}−{sinx}}{\left(\sqrt{\mathrm{1}+{tgx}}+\sqrt{\mathrm{1}+{sinx}}\right){x}^{\mathrm{3}} }= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{2}}}{\left(\sqrt{\mathrm{1}+\mathrm{0}}+\sqrt{\mathrm{1}+\mathrm{0}}\right){x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{4}}. \\ $$$$ \\ $$
Commented by Joel576 last updated on 22/Mar/17
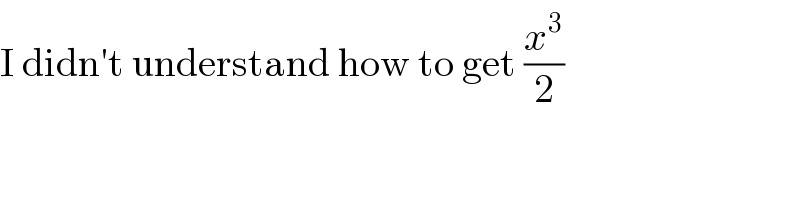
$$\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\frac{{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$
Commented by sm3l2996 last updated on 22/Mar/17
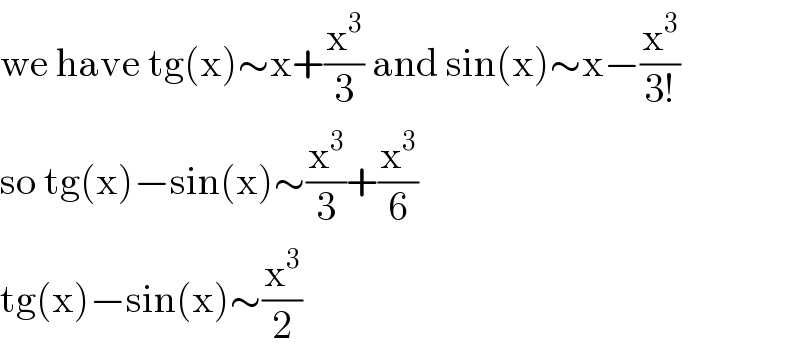
$$\mathrm{we}\:\mathrm{have}\:\mathrm{tg}\left(\mathrm{x}\right)\sim\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:\mathrm{and}\:\mathrm{sin}\left(\mathrm{x}\right)\sim\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!} \\ $$$$\mathrm{so}\:\mathrm{tg}\left(\mathrm{x}\right)−\mathrm{sin}\left(\mathrm{x}\right)\sim\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\mathrm{tg}\left(\mathrm{x}\right)−\mathrm{sin}\left(\mathrm{x}\right)\sim\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}} \\ $$
Commented by sandy_suhendra last updated on 22/Mar/17
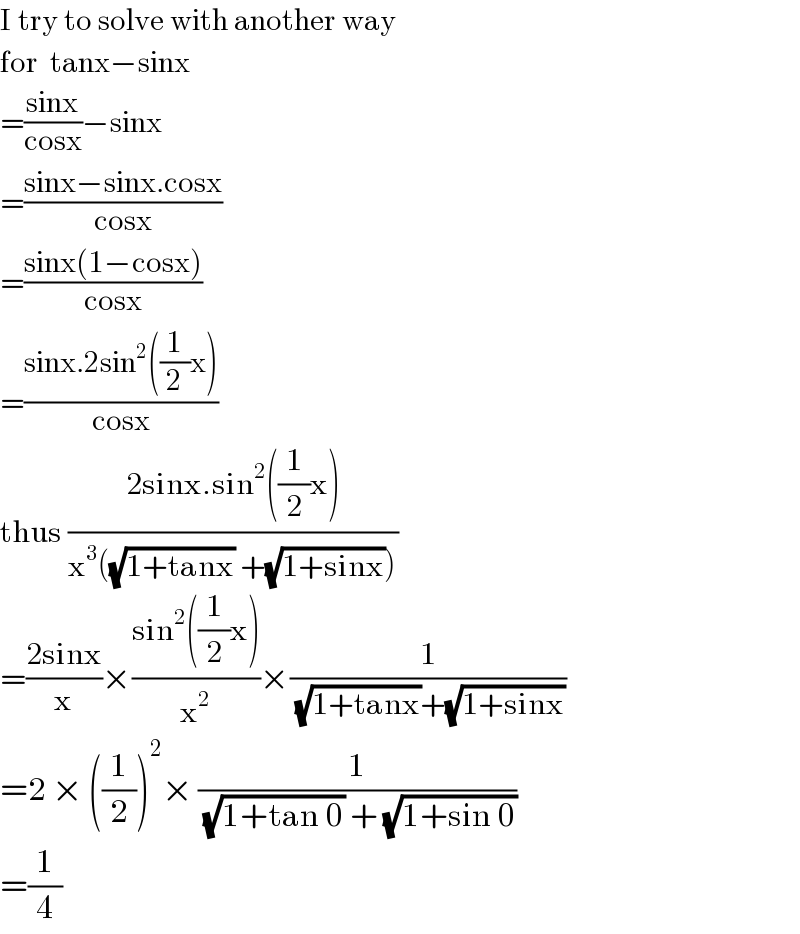
$$\mathrm{I}\:\mathrm{try}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{with}\:\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{for}\:\:\mathrm{tanx}−\mathrm{sinx} \\ $$$$=\frac{\mathrm{sinx}}{\mathrm{cosx}}−\mathrm{sinx} \\ $$$$=\frac{\mathrm{sinx}−\mathrm{sinx}.\mathrm{cosx}}{\mathrm{cosx}} \\ $$$$=\frac{\mathrm{sinx}\left(\mathrm{1}−\mathrm{cosx}\right)}{\mathrm{cosx}} \\ $$$$=\frac{\mathrm{sinx}.\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}{\mathrm{cosx}} \\ $$$$\mathrm{thus}\:\frac{\mathrm{2sinx}.\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}{\mathrm{x}^{\mathrm{3}} \left(\sqrt{\mathrm{1}+\mathrm{tanx}}\:+\sqrt{\mathrm{1}+\mathrm{sinx}}\right)} \\ $$$$=\frac{\mathrm{2sinx}}{\mathrm{x}}×\frac{\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tanx}}+\sqrt{\mathrm{1}+\mathrm{sinx}}} \\ $$$$=\mathrm{2}\:×\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ×\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{tan}\:\mathrm{0}}\:+\:\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{0}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Joel576 last updated on 23/Mar/17
$${thank}\:{you}\:{very}\:{much} \\ $$
