Question Number 113557 by Aina Samuel Temidayo last updated on 14/Sep/20

$$\mathrm{If}\:\mathrm{the}\:\mathrm{numerically}\:\mathrm{smaller}\:\mathrm{root}\:\mathrm{of}\: \\ $$$${x}^{\mathrm{2}} +{mx}=\mathrm{2}\:\mathrm{is}\:\mathrm{more}\:\mathrm{than}\:\mathrm{the}\:\mathrm{other}\:\mathrm{one}, \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{m}. \\ $$
Answered by mr W last updated on 14/Sep/20
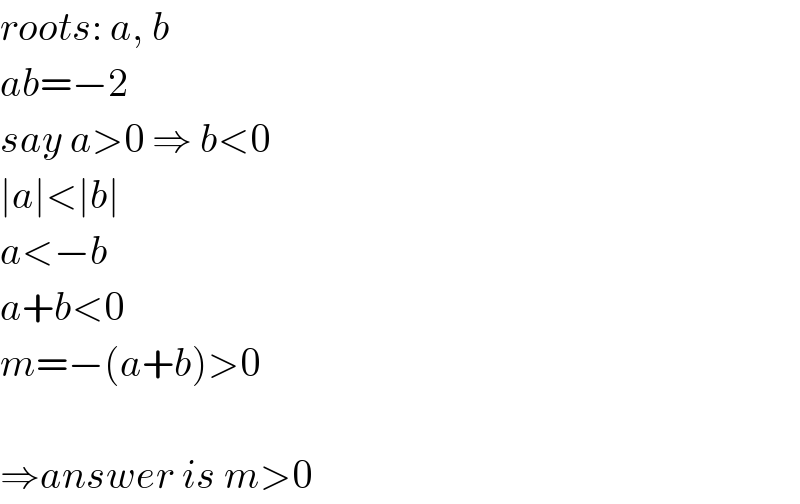
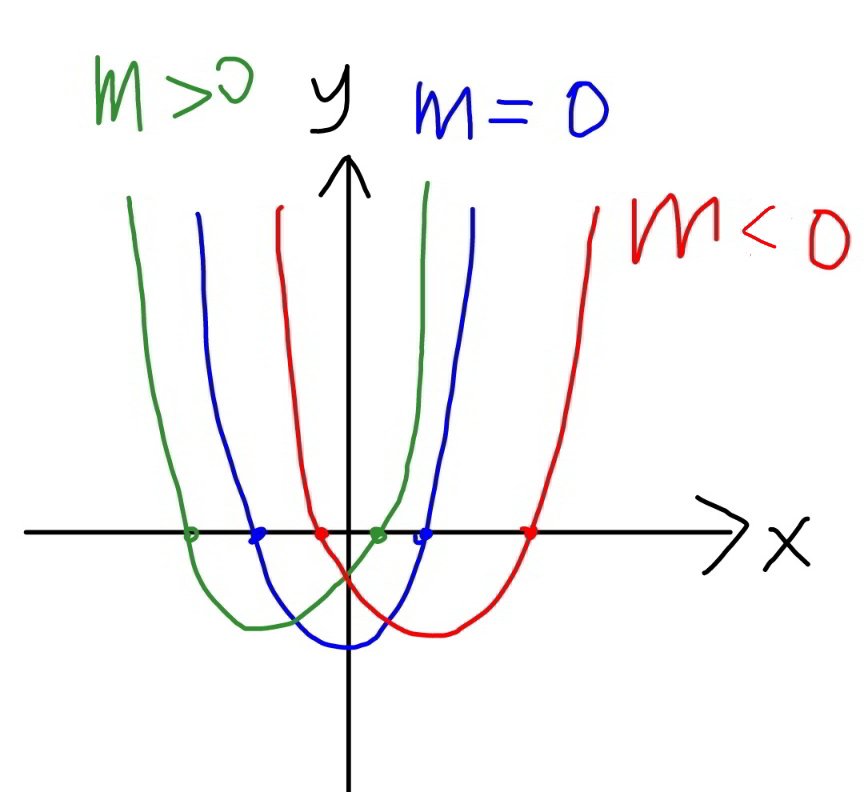
$${roots}:\:{a},\:{b} \\ $$$${ab}=−\mathrm{2} \\ $$$${say}\:{a}>\mathrm{0}\:\Rightarrow\:{b}<\mathrm{0} \\ $$$$\mid{a}\mid<\mid{b}\mid \\ $$$${a}<−{b} \\ $$$${a}+{b}<\mathrm{0} \\ $$$${m}=−\left({a}+{b}\right)>\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{answer}\:{is}\:{m}>\mathrm{0} \\ $$
Commented by mr W last updated on 14/Sep/20