
Question Number 113488 by weltr last updated on 13/Sep/20
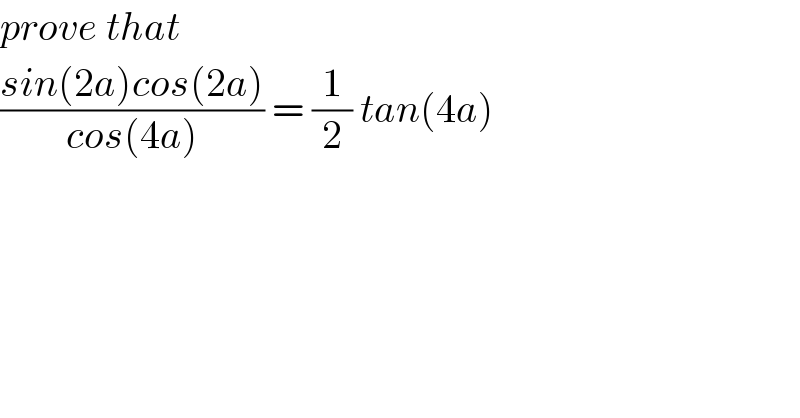
$${prove}\:{that} \\ $$$$\frac{{sin}\left(\mathrm{2}{a}\right){cos}\left(\mathrm{2}{a}\right)}{{cos}\left(\mathrm{4}{a}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:{tan}\left(\mathrm{4}{a}\right) \\ $$
Answered by som(math1967) last updated on 13/Sep/20
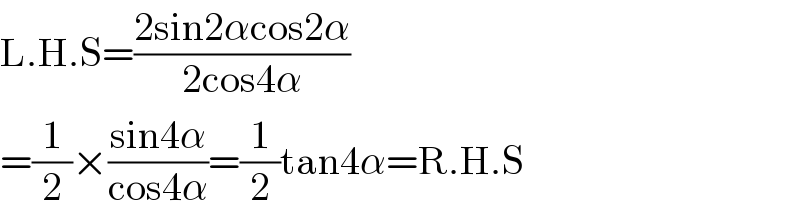
$$\mathrm{L}.\mathrm{H}.\mathrm{S}=\frac{\mathrm{2sin2}\alpha\mathrm{cos2}\alpha}{\mathrm{2cos4}\alpha} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{sin4}\alpha}{\mathrm{cos4}\alpha}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan4}\alpha=\mathrm{R}.\mathrm{H}.\mathrm{S} \\ $$
Commented by weltr last updated on 13/Sep/20

$${thanks} \\ $$
Answered by floor(10²Eta[1]) last updated on 13/Sep/20
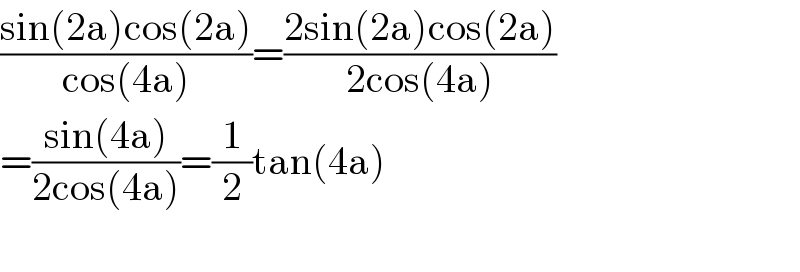
$$\frac{\mathrm{sin}\left(\mathrm{2a}\right)\mathrm{cos}\left(\mathrm{2a}\right)}{\mathrm{cos}\left(\mathrm{4a}\right)}=\frac{\mathrm{2sin}\left(\mathrm{2a}\right)\mathrm{cos}\left(\mathrm{2a}\right)}{\mathrm{2cos}\left(\mathrm{4a}\right)} \\ $$$$=\frac{\mathrm{sin}\left(\mathrm{4a}\right)}{\mathrm{2cos}\left(\mathrm{4a}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\left(\mathrm{4a}\right) \\ $$$$ \\ $$
Commented by weltr last updated on 13/Sep/20

$${thanks} \\ $$
