
Question Number 11338 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Mar/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Mar/17
Answered by mrW1 last updated on 21/Mar/17

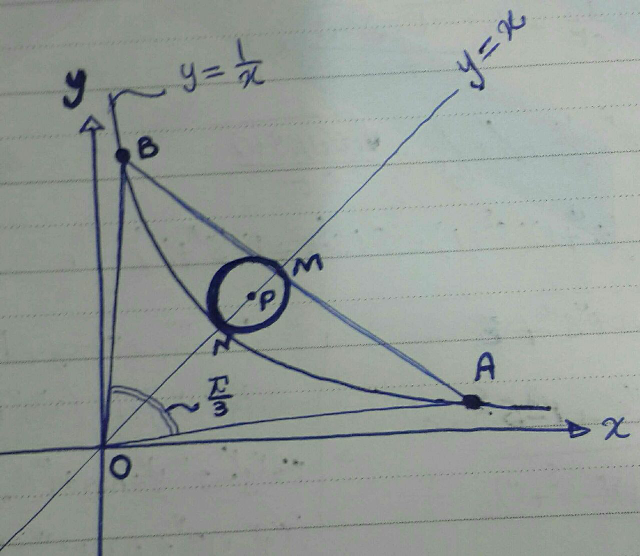
$$\left(\mathrm{1}\right) \\ $$$${let}\:{B}\left({t},\frac{\mathrm{1}}{{t}}\right) \\ $$$$\boldsymbol{{a}}=\overset{\rightarrow} {{OA}} \\ $$$$\boldsymbol{{b}}=\overset{\rightarrow} {{OB}} \\ $$$$\mathrm{cos}\:\angle{AOB}=\frac{\boldsymbol{{a}}\centerdot\boldsymbol{{b}}}{\mid\boldsymbol{{a}}\mid×\mid\boldsymbol{{b}}\mid}=\frac{{t}\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{{t}\sqrt{\mathrm{3}}}}{\sqrt{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }×\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}=\mathrm{cos}\:\frac{\pi}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{t}\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{{t}\sqrt{\mathrm{3}}}}{\sqrt{\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }×\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}{t}+\frac{\mathrm{1}}{{t}}}{\sqrt{\mathrm{10}}×\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{3}{t}+\frac{\mathrm{1}}{{t}}=\frac{\sqrt{\mathrm{10}}}{\mathrm{2}}×\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }} \\ $$$$\mathrm{9}{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{6}=\frac{\mathrm{10}}{\mathrm{4}}\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right) \\ $$$$\mathrm{9}{t}^{\mathrm{4}} +\mathrm{1}+\mathrm{6}{t}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{2}}\left({t}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$$\mathrm{13}{t}^{\mathrm{4}} +\mathrm{12}{t}^{\mathrm{2}} −\mathrm{3}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} =\frac{−\mathrm{12}+\sqrt{\mathrm{144}+\mathrm{4}×\mathrm{13}×\mathrm{3}}}{\mathrm{2}×\mathrm{13}}=\frac{\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{6}}{\mathrm{13}} \\ $$$${t}=\sqrt{\frac{\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{6}}{\mathrm{13}}} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Apr/17

$${part}#\mathrm{1} \\ $$$${AB}^{\mathrm{2}} ={oA}^{\mathrm{2}} +{oB}^{\mathrm{2}} −\mathrm{2}{oA}.{oB}.{cos}\measuredangle{AoB}\:\:\:\:\: \\ $$$$\left({s}−{t}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{s}}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} =\left({s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} }\right)+\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)−\mathrm{2}\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}}{{s}}.\frac{\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}}{{t}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Rightarrow \\ $$$$−\mathrm{2}\left({st}+\frac{\mathrm{1}}{{st}}\right)=−\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}.\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}}{{st}}\Rightarrow \\ $$$$\mathrm{2}\left({s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}\right)=\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}.\sqrt{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\mathrm{4}{s}^{\mathrm{4}} {t}^{\mathrm{4}} +\mathrm{8}{s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{4}=\left({s}^{\mathrm{4}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}\right)={s}^{\mathrm{4}} {t}^{\mathrm{4}} +{s}^{\mathrm{4}} +{t}^{\mathrm{4}} +\mathrm{1}\Rightarrow \\ $$$$\left(\mathrm{3}{s}^{\mathrm{4}} −\mathrm{1}\right){t}^{\mathrm{4}} +\mathrm{8}{s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{3}−{s}^{\mathrm{4}} =\mathrm{0}\Rightarrow \\ $$$${t}^{\mathrm{2}} =\frac{−\mathrm{8}{s}^{\mathrm{2}} +\sqrt{\mathrm{64}{s}^{\mathrm{4}} −\mathrm{4}\left(\mathrm{3}{s}^{\mathrm{4}} −\mathrm{1}\right)\left(\mathrm{3}−{s}^{\mathrm{4}} \right)}}{\mathrm{2}\left(\mathrm{3}{s}^{\mathrm{4}} −\mathrm{1}\right)}= \\ $$$${t}^{\mathrm{2}} =\frac{−\mathrm{8}{s}^{\mathrm{2}} +\sqrt{\mathrm{12}\left({s}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{3}{s}^{\mathrm{4}} −\mathrm{1}\right)}=\frac{\sqrt{\mathrm{3}}\left({s}^{\mathrm{4}} +\mathrm{1}\right)−\mathrm{4}{s}^{\mathrm{2}} }{\mathrm{3}{s}^{\mathrm{4}} −\mathrm{1}} \\ $$$${t}^{\mathrm{2}} =\frac{\left({s}^{\mathrm{2}} −\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\sqrt{\mathrm{3}}{s}^{\mathrm{2}} +\mathrm{1}\right)\left(\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{{s}^{\mathrm{2}} −\sqrt{\mathrm{3}}}{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} +\mathrm{1}}\left({in}\:{general}\right) \\ $$$$\left.{i}\right).\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}\neq\mathrm{0}\Rightarrow{s}\neq\frac{\mathrm{1}}{\sqrt[{\mathrm{4}}]{\mathrm{3}}}. \\ $$$$\left.{ii}\right).{s}^{\mathrm{2}} −\sqrt{\mathrm{3}}>\mathrm{0}\Rightarrow{s}>\sqrt[{\mathrm{4}}]{\mathrm{3}}\:. \\ $$$$\left.{iii}\right).{s}=\sqrt{\mathrm{3}}\Rightarrow{t}^{\mathrm{2}} =\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{}\mathrm{3}+\mathrm{1}} \\ $$$$\boldsymbol{{t}}=\sqrt{\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}}}.\boldsymbol{{B}}\left(\sqrt[{�}]{\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}}},\sqrt{\frac{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{3}−\sqrt{\mathrm{3}}}}\right). \\ $$$$\mathrm{2}.{m}_{{AB}} =\frac{{y}_{{B}} −{y}_{{A}} }{{x}_{{B}} −{x}_{{A}} }=\frac{\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{s}}}{{t}−{s}}=\frac{−\mathrm{1}}{{st}} \\ $$$${y}−{y}_{{B}} ={m}_{{AB}} \left({x}−{x}_{{B}} \right)\Rightarrow{y}−\frac{\mathrm{1}}{{t}}=\frac{−\mathrm{1}}{{st}}\left({x}−{t}\right) \\ $$$${sty}−{s}=−\left({x}−{t}\right)\Rightarrow{sty}−{s}=−{x}+{t} \\ $$$${AB}:\:{sty}=−{x}+{s}+{t}. \\ $$$${oN}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\sqrt{\mathrm{2}} \\ $$$${intersect}\:{of}\:{AB}\:{and}\:{circle}\:{not}\:{lie}\:{on}\: \\ $$$${y}={x}\:{in}\:{all}\:{cases}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Mar/17
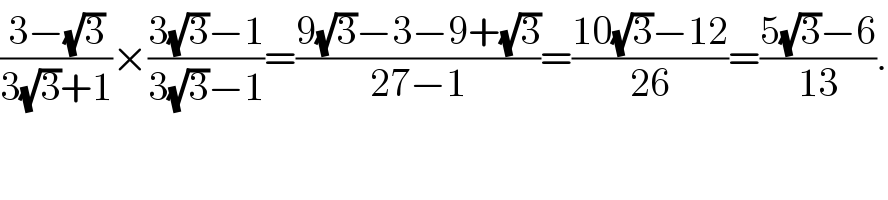
$$\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}}×\frac{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}}=\frac{\mathrm{9}\sqrt{\mathrm{3}}−\mathrm{3}−\mathrm{9}+\sqrt{\mathrm{3}}}{\mathrm{27}−\mathrm{1}}=\frac{\mathrm{10}\sqrt{\mathrm{3}}−\mathrm{12}}{\mathrm{26}}=\frac{\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{6}}{\mathrm{13}}. \\ $$
Commented by mrW1 last updated on 22/Mar/17

$$\mathscr{G}{ood}! \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Apr/17
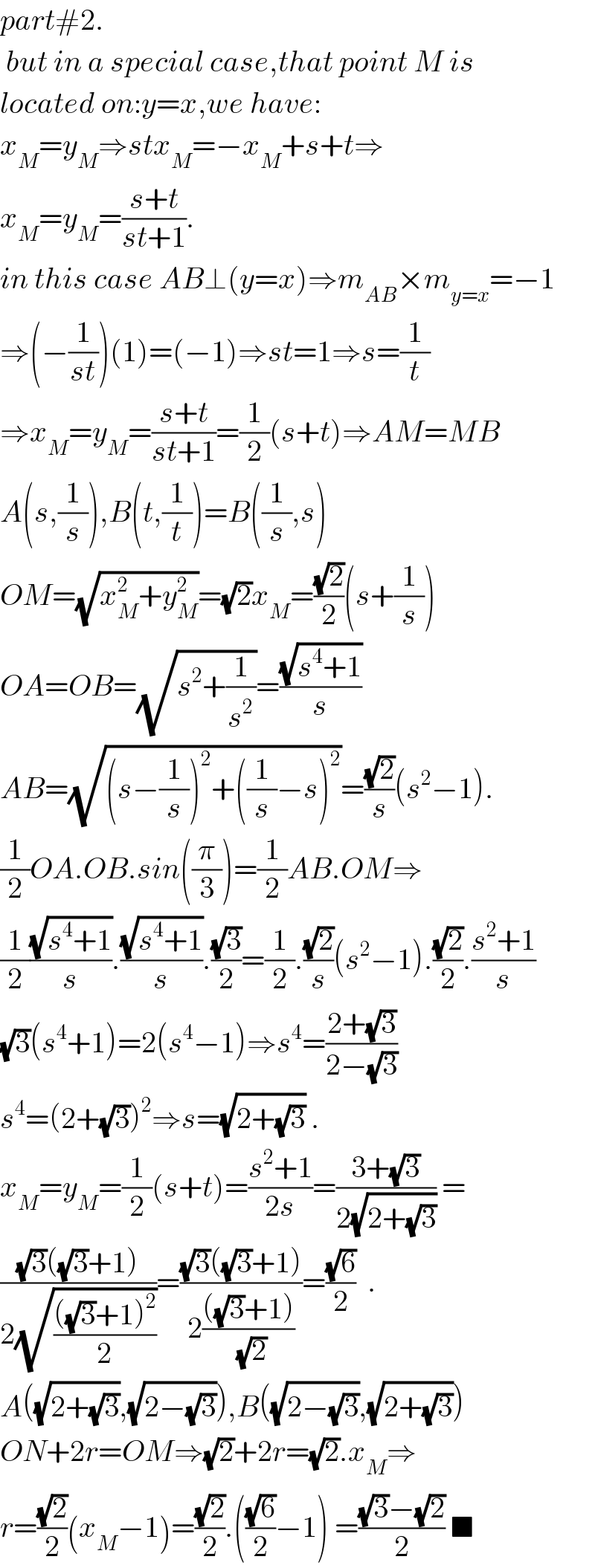
$${part}#\mathrm{2}.\: \\ $$$$\:{but}\:{in}\:{a}\:{special}\:{case},{that}\:{point}\:{M}\:{is} \\ $$$${located}\:{on}:{y}={x},{we}\:{have}: \\ $$$${x}_{{M}} ={y}_{{M}} \Rightarrow{stx}_{{M}} =−{x}_{{M}} +{s}+{t}\Rightarrow \\ $$$${x}_{{M}} ={y}_{{M}} =\frac{{s}+{t}}{{st}+\mathrm{1}}. \\ $$$${in}\:{this}\:{case}\:{AB}\bot\left({y}={x}\right)\Rightarrow{m}_{{AB}} ×{m}_{{y}={x}} =−\mathrm{1} \\ $$$$\Rightarrow\left(−\frac{\mathrm{1}}{{st}}\right)\left(\mathrm{1}\right)=\left(−\mathrm{1}\right)\Rightarrow{st}=\mathrm{1}\Rightarrow{s}=\frac{\mathrm{1}}{{t}} \\ $$$$\Rightarrow{x}_{{M}} ={y}_{{M}} =\frac{{s}+{t}}{{st}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left({s}+{t}\right)\Rightarrow{AM}={MB} \\ $$$${A}\left({s},\frac{\mathrm{1}}{{s}}\right),{B}\left({t},\frac{\mathrm{1}}{{t}}\right)={B}\left(\frac{\mathrm{1}}{{s}},{s}\right) \\ $$$${OM}=\sqrt{{x}_{{M}} ^{\mathrm{2}} +{y}_{{M}} ^{\mathrm{2}} }=\sqrt{\mathrm{2}}{x}_{{M}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({s}+\frac{\mathrm{1}}{{s}}\right) \\ $$$${OA}={OB}=\sqrt{{s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} }}=\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}}{{s}} \\ $$$${AB}=\sqrt{\left({s}−\frac{\mathrm{1}}{{s}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{s}}−{s}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{2}}}{{s}}\left({s}^{\mathrm{2}} −\mathrm{1}\right). \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{OA}.{OB}.{sin}\left(\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{AB}.{OM}\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}}{{s}}.\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}}{{s}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\sqrt{\mathrm{2}}}{{s}}\left({s}^{\mathrm{2}} −\mathrm{1}\right).\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\frac{{s}^{\mathrm{2}} +\mathrm{1}}{{s}} \\ $$$$\sqrt{\mathrm{3}}\left({s}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{2}\left({s}^{\mathrm{4}} −\mathrm{1}\right)\Rightarrow{s}^{\mathrm{4}} =\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$${s}^{\mathrm{4}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \Rightarrow{s}=\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:. \\ $$$${x}_{{M}} ={y}_{{M}} =\frac{\mathrm{1}}{\mathrm{2}}\left({s}+{t}\right)=\frac{{s}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}{s}}=\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}\:= \\ $$$$\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{2}\sqrt{\frac{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}}}=\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{2}\frac{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)}{\sqrt{\mathrm{2}}}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}\:\:. \\ $$$${A}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}},\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right),{B}\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}},\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right) \\ $$$${ON}+\mathrm{2}{r}={OM}\Rightarrow\sqrt{\mathrm{2}}+\mathrm{2}{r}=\sqrt{\mathrm{2}}.{x}_{{M}} \Rightarrow \\ $$$${r}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left({x}_{{M}} −\mathrm{1}\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\left(\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}−\mathrm{1}\right)\:=\frac{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\mathrm{2}}\:\blacksquare \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Apr/17
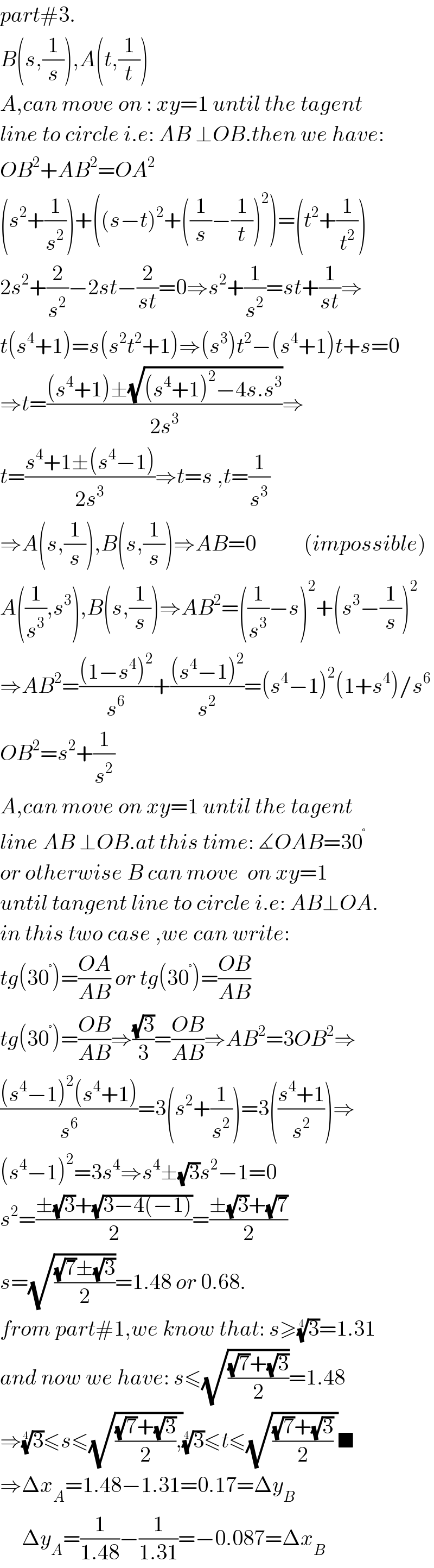
$${part}#\mathrm{3}. \\ $$$${B}\left({s},\frac{\mathrm{1}}{{s}}\right),{A}\left({t},\frac{\mathrm{1}}{{t}}\right) \\ $$$${A},{can}\:{move}\:{on}\::\:{xy}=\mathrm{1}\:{until}\:{the}\:{tagent} \\ $$$${line}\:{to}\:{circle}\:{i}.{e}:\:{AB}\:\bot{OB}.{then}\:{we}\:{have}: \\ $$$${OB}^{\mathrm{2}} +{AB}^{\mathrm{2}} ={OA}^{\mathrm{2}} \\ $$$$\left({s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} }\right)+\left(\left({s}−{t}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{s}}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} \right)=\left({t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right) \\ $$$$\mathrm{2}{s}^{\mathrm{2}} +\frac{\mathrm{2}}{{s}^{\mathrm{2}} }−\mathrm{2}{st}−\frac{\mathrm{2}}{{st}}=\mathrm{0}\Rightarrow{s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} }={st}+\frac{\mathrm{1}}{{st}}\Rightarrow \\ $$$${t}\left({s}^{\mathrm{4}} +\mathrm{1}\right)={s}\left({s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}\right)\Rightarrow\left({s}^{\mathrm{3}} \right){t}^{\mathrm{2}} −\left({s}^{\mathrm{4}} +\mathrm{1}\right){t}+{s}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\left({s}^{\mathrm{4}} +\mathrm{1}\right)\pm\sqrt{\left({s}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{s}.{s}^{\mathrm{3}} }}{\mathrm{2}{s}^{\mathrm{3}} }\Rightarrow \\ $$$${t}=\frac{{s}^{\mathrm{4}} +\mathrm{1}\pm\left({s}^{\mathrm{4}} −\mathrm{1}\right)}{\mathrm{2}{s}^{\mathrm{3}} }\Rightarrow{t}={s}\:,{t}=\frac{\mathrm{1}}{{s}^{\mathrm{3}} } \\ $$$$\Rightarrow{A}\left({s},\frac{\mathrm{1}}{{s}}\right),{B}\left({s},\frac{\mathrm{1}}{{s}}\right)\Rightarrow{AB}=\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\left({impossible}\right) \\ $$$${A}\left(\frac{\mathrm{1}}{{s}^{\mathrm{3}} },{s}^{\mathrm{3}} \right),{B}\left({s},\frac{\mathrm{1}}{{s}}\right)\Rightarrow{AB}^{\mathrm{2}} =\left(\frac{\mathrm{1}}{{s}^{\mathrm{3}} }−{s}\right)^{\mathrm{2}} +\left({s}^{\mathrm{3}} −\frac{\mathrm{1}}{{s}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{AB}^{\mathrm{2}} =\frac{\left(\mathrm{1}−{s}^{\mathrm{4}} \right)^{\mathrm{2}} }{{s}^{\mathrm{6}} }+\frac{\left({s}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} }{{s}^{\mathrm{2}} }=\left({s}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+{s}^{\mathrm{4}} \right)/{s}^{\mathrm{6}} \\ $$$${OB}^{\mathrm{2}} ={s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} } \\ $$$${A},{can}\:{move}\:{on}\:{xy}=\mathrm{1}\:{until}\:{the}\:{tagent} \\ $$$${line}\:{AB}\:\bot{OB}.{at}\:{this}\:{time}:\:\measuredangle{OAB}=\mathrm{30}^{°} \\ $$$${or}\:{otherwise}\:{B}\:{can}\:{move}\:\:{on}\:{xy}=\mathrm{1} \\ $$$${until}\:{tangent}\:{line}\:{to}\:{circle}\:{i}.{e}:\:{AB}\bot{OA}. \\ $$$${in}\:{this}\:{two}\:{case}\:,{we}\:{can}\:{write}: \\ $$$${tg}\left(\mathrm{30}^{°} \right)=\frac{{OA}}{{AB}}\:{or}\:{tg}\left(\mathrm{30}^{°} \right)=\frac{{OB}}{{AB}} \\ $$$${tg}\left(\mathrm{30}^{°} \right)=\frac{{OB}}{{AB}}\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}=\frac{{OB}}{{AB}}\Rightarrow{AB}^{\mathrm{2}} =\mathrm{3}{OB}^{\mathrm{2}} \Rightarrow \\ $$$$\frac{\left({s}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} \left({s}^{\mathrm{4}} +\mathrm{1}\right)}{{s}^{\mathrm{6}} }=\mathrm{3}\left({s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} }\right)=\mathrm{3}\left(\frac{{s}^{\mathrm{4}} +\mathrm{1}}{{s}^{\mathrm{2}} }\right)\Rightarrow \\ $$$$\left({s}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}{s}^{\mathrm{4}} \Rightarrow{s}^{\mathrm{4}} \pm\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$${s}^{\mathrm{2}} =\frac{\pm\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}−\mathrm{4}\left(−\mathrm{1}\right)}}{\mathrm{2}}=\frac{\pm\sqrt{\mathrm{3}}+\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$$${s}=\sqrt{\frac{\sqrt{\mathrm{7}}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}}=\mathrm{1}.\mathrm{48}\:{or}\:\mathrm{0}.\mathrm{68}. \\ $$$${from}\:{part}#\mathrm{1},{we}\:{know}\:{that}:\:{s}\geqslant\sqrt[{\mathrm{4}}]{\mathrm{3}}=\mathrm{1}.\mathrm{31} \\ $$$${and}\:{now}\:{we}\:{have}:\:{s}\leqslant\sqrt{\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}}=\mathrm{1}.\mathrm{48} \\ $$$$\Rightarrow\sqrt[{\mathrm{4}}]{\mathrm{3}}\leqslant{s}\leqslant\sqrt{\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}},}\sqrt[{\mathrm{4}}]{\mathrm{3}}\leqslant{t}\leqslant\sqrt{\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:}\blacksquare \\ $$$$\Rightarrow\Delta{x}_{{A}} =\mathrm{1}.\mathrm{48}−\mathrm{1}.\mathrm{31}=\mathrm{0}.\mathrm{17}=\Delta{y}_{{B}} \\ $$$$\:\:\:\:\:\Delta{y}_{{A}} =\frac{\mathrm{1}}{\mathrm{1}.\mathrm{48}}−\frac{\mathrm{1}}{\mathrm{1}.\mathrm{31}}=−\mathrm{0}.\mathrm{087}=\Delta{x}_{{B}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 07/Apr/17
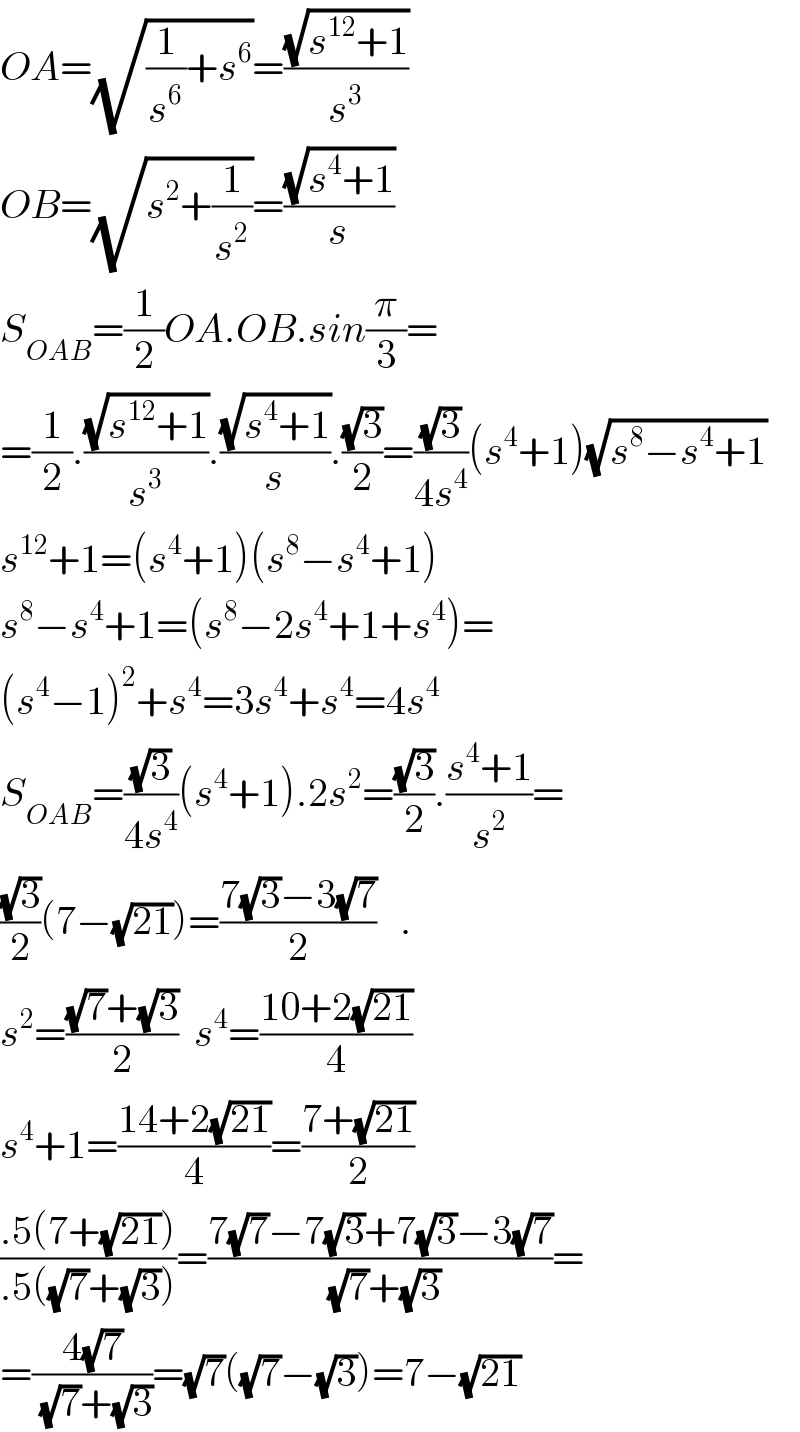
$${OA}=\sqrt{\frac{\mathrm{1}}{{s}^{\mathrm{6}} }+{s}^{\mathrm{6}} }=\frac{\sqrt{{s}^{\mathrm{12}} +\mathrm{1}}}{{s}^{\mathrm{3}} } \\ $$$${OB}=\sqrt{{s}^{\mathrm{2}} +\frac{\mathrm{1}}{{s}^{\mathrm{2}} }}=\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}}{{s}} \\ $$$${S}_{{OAB}} =\frac{\mathrm{1}}{\mathrm{2}}{OA}.{OB}.{sin}\frac{\pi}{\mathrm{3}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\sqrt{{s}^{\mathrm{12}} +\mathrm{1}}}{{s}^{\mathrm{3}} }.\frac{\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}}{{s}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}{s}^{\mathrm{4}} }\left({s}^{\mathrm{4}} +\mathrm{1}\right)\sqrt{{s}^{\mathrm{8}} −{s}^{\mathrm{4}} +\mathrm{1}} \\ $$$${s}^{\mathrm{12}} +\mathrm{1}=\left({s}^{\mathrm{4}} +\mathrm{1}\right)\left({s}^{\mathrm{8}} −{s}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$${s}^{\mathrm{8}} −{s}^{\mathrm{4}} +\mathrm{1}=\left({s}^{\mathrm{8}} −\mathrm{2}{s}^{\mathrm{4}} +\mathrm{1}+{s}^{\mathrm{4}} \right)= \\ $$$$\left({s}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} +{s}^{\mathrm{4}} =\mathrm{3}{s}^{\mathrm{4}} +{s}^{\mathrm{4}} =\mathrm{4}{s}^{\mathrm{4}} \\ $$$${S}_{{OAB}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}{s}^{\mathrm{4}} }\left({s}^{\mathrm{4}} +\mathrm{1}\right).\mathrm{2}{s}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{{s}^{\mathrm{4}} +\mathrm{1}}{{s}^{\mathrm{2}} }= \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{7}−\sqrt{\mathrm{21}}\right)=\frac{\mathrm{7}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{7}}}{\mathrm{2}}\:\:\:. \\ $$$${s}^{\mathrm{2}} =\frac{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{s}^{\mathrm{4}} =\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{4}} \\ $$$${s}^{\mathrm{4}} +\mathrm{1}=\frac{\mathrm{14}+\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{4}}=\frac{\mathrm{7}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\frac{.\mathrm{5}\left(\mathrm{7}+\sqrt{\mathrm{21}}\right)}{.\mathrm{5}\left(\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}\right)}=\frac{\mathrm{7}\sqrt{\mathrm{7}}−\mathrm{7}\sqrt{\mathrm{3}}+\mathrm{7}\sqrt{\mathrm{3}}−\mathrm{3}\sqrt{\mathrm{7}}}{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}= \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{7}}}{\sqrt{\mathrm{7}}+\sqrt{\mathrm{3}}}=\sqrt{\mathrm{7}}\left(\sqrt{\mathrm{7}}−\sqrt{\mathrm{3}}\right)=\mathrm{7}−\sqrt{\mathrm{21}} \\ $$
Commented by ridwan balatif last updated on 09/Apr/17
$$\mathrm{Ngomong}\:\mathrm{opo}\:\mathrm{sih}\:\mathrm{kalian}\:\mathrm{ini}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Apr/17
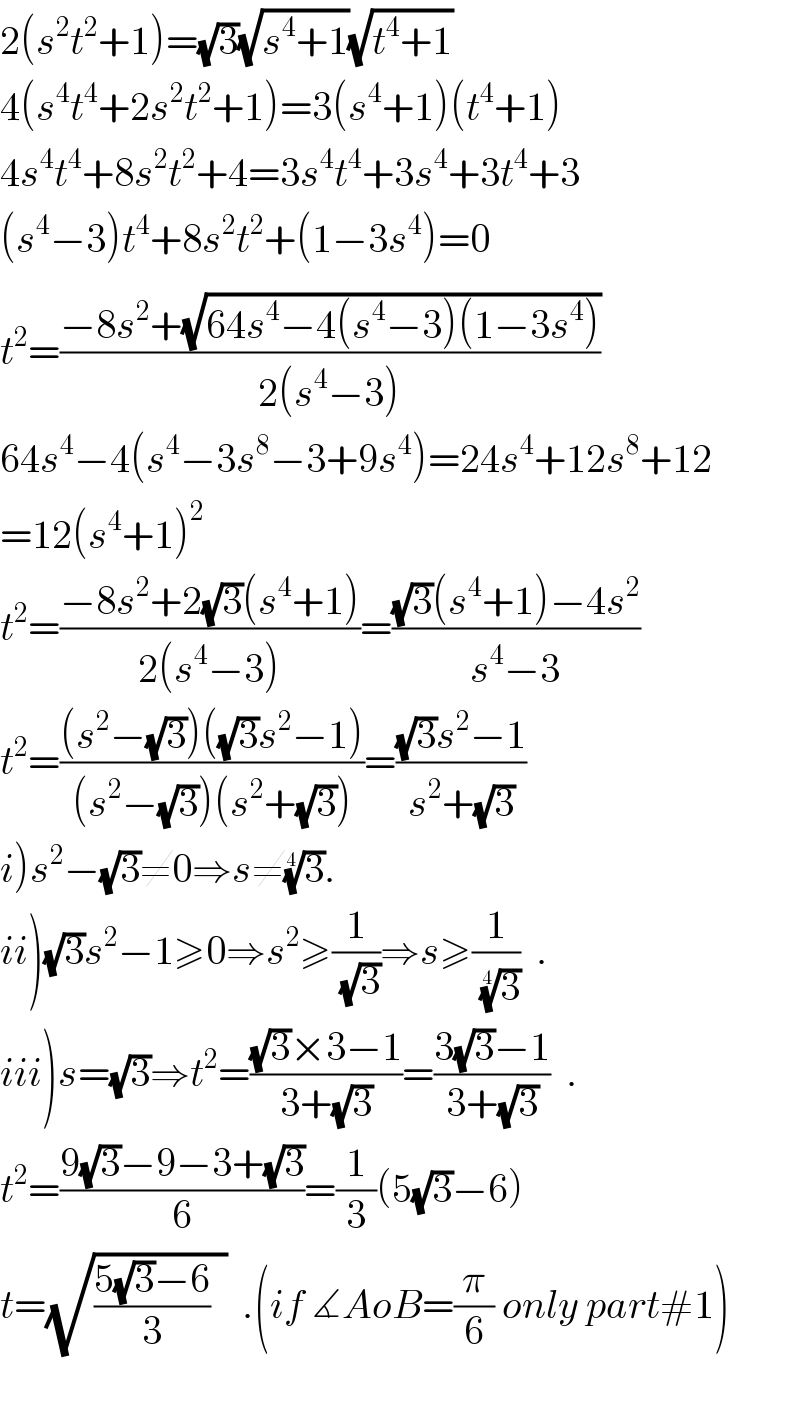
$$\mathrm{2}\left({s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}\right)=\sqrt{\mathrm{3}}\sqrt{{s}^{\mathrm{4}} +\mathrm{1}}\sqrt{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\mathrm{4}\left({s}^{\mathrm{4}} {t}^{\mathrm{4}} +\mathrm{2}{s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{3}\left({s}^{\mathrm{4}} +\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$$\mathrm{4}{s}^{\mathrm{4}} {t}^{\mathrm{4}} +\mathrm{8}{s}^{\mathrm{2}} {t}^{\mathrm{2}} +\mathrm{4}=\mathrm{3}{s}^{\mathrm{4}} {t}^{\mathrm{4}} +\mathrm{3}{s}^{\mathrm{4}} +\mathrm{3}{t}^{\mathrm{4}} +\mathrm{3} \\ $$$$\left({s}^{\mathrm{4}} −\mathrm{3}\right){t}_{} ^{\mathrm{4}} +\mathrm{8}{s}^{\mathrm{2}} {t}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{3}{s}^{\mathrm{4}} \right)=\mathrm{0} \\ $$$${t}^{\mathrm{2}} =\frac{−\mathrm{8}{s}^{\mathrm{2}} +\sqrt{\mathrm{64}{s}^{\mathrm{4}} −\mathrm{4}\left({s}^{\mathrm{4}} −\mathrm{3}\right)\left(\mathrm{1}−\mathrm{3}{s}^{\mathrm{4}} \right)}}{\mathrm{2}\left({s}^{\mathrm{4}} −\mathrm{3}\right)} \\ $$$$\mathrm{64}{s}^{\mathrm{4}} −\mathrm{4}\left({s}^{\mathrm{4}} −\mathrm{3}{s}^{\mathrm{8}} −\mathrm{3}+\mathrm{9}{s}^{\mathrm{4}} \right)=\mathrm{24}{s}^{\mathrm{4}} +\mathrm{12}{s}^{\mathrm{8}} +\mathrm{12} \\ $$$$=\mathrm{12}\left({s}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} =\frac{−\mathrm{8}{s}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\left({s}^{\mathrm{4}} +\mathrm{1}\right)}{\mathrm{2}\left({s}^{\mathrm{4}} −\mathrm{3}\right)}=\frac{\sqrt{\mathrm{3}}\left({s}^{\mathrm{4}} +\mathrm{1}\right)−\mathrm{4}{s}^{\mathrm{2}} }{{s}^{\mathrm{4}} −\mathrm{3}} \\ $$$${t}^{\mathrm{2}} =\frac{\left({s}^{\mathrm{2}} −\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}\right)}{\left({s}^{\mathrm{2}} −\sqrt{\mathrm{3}}\right)\left({s}^{\mathrm{2}} +\sqrt{\mathrm{3}}\right)}=\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}}{{s}^{\mathrm{2}} +\sqrt{\mathrm{3}}} \\ $$$$\left.{i}\right){s}^{\mathrm{2}} −\sqrt{\mathrm{3}}\neq\mathrm{0}\Rightarrow{s}\neq\sqrt[{\mathrm{4}}]{\mathrm{3}}. \\ $$$$\left.{ii}\right)\sqrt{\mathrm{3}}{s}^{\mathrm{2}} −\mathrm{1}\geqslant\mathrm{0}\Rightarrow{s}^{\mathrm{2}} \geqslant\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\Rightarrow{s}\geqslant\frac{\mathrm{1}}{\sqrt[{\mathrm{4}}]{\mathrm{3}}}\:\:. \\ $$$$\left.{iii}\right){s}=\sqrt{\mathrm{3}}\Rightarrow{t}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}×\mathrm{3}−\mathrm{1}}{\mathrm{3}+\sqrt{\mathrm{3}}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{3}+\sqrt{\mathrm{3}}}\:\:. \\ $$$${t}^{\mathrm{2}} =\frac{\mathrm{9}\sqrt{\mathrm{3}}−\mathrm{9}−\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{6}\right) \\ $$$${t}=\sqrt{\frac{\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{6}}{\mathrm{3}}\:\:}\:\:.\left({if}\:\measuredangle{AoB}=\frac{\pi}{\mathrm{6}}\:{only}\:{part}#\mathrm{1}\right) \\ $$$$ \\ $$
