Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

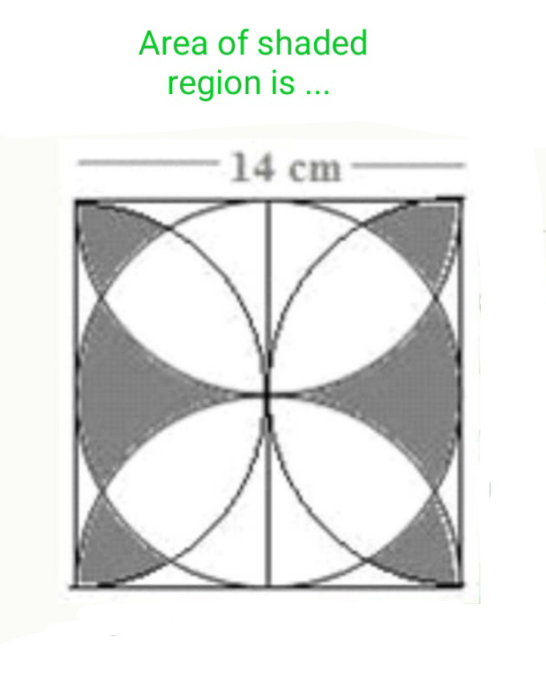
Question Number 113219 by naka3546 last updated on 11/Sep/20

Answered by 1549442205PVT last updated on 11/Sep/20

Commented by Aina Samuel Temidayo last updated on 11/Sep/20

Please how do you construct these things?

$$\mathrm{Please}\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{construct}\:\mathrm{these} \\ $$$$\mathrm{things}? \\ $$

Commented by 1549442205PVT last updated on 12/Sep/20

It is easy to see that FK^(⌢) =KL^(⌢) =LG^(⌢) =GN^(⌢) =NJ^(⌢) =JE^(⌢) =(π/6)⇒FEK^(�) =15° The area of the sector IKF is S_(sectorIKF) =((πR^2 )/(12))=((49π)/(12)).The are of the equalateral triangle IKG is S_(ΔIKG) =((R^2 (√3))/4)=((49(√3))/4).The area of curve triangle DKF equal to S_(DGIF) −2.S_(sector) −S_(ΔIKG) =49−((49π)/6)−((49(√3))/4)(1) .The area of the sector ILM is S_(sectorILM) =((πR^2 )/3)=((49π)/3)(since LFM^(⌢) =120°) S_(ΔILM) =S_(ΔIKG) =((49(√3))/4).Hence,the area of part is limited by the LIM^(⌢) and the arc LFM^(⌢) is 2(S_(sectorILM) −S_(ΔILM) ) =2(((49π)/3)−((49(√3))/4))(2) The are of eight curve white triangle are S_1 =8(49−((49π)/6)−((49(√3))/4))(3).The area of two big white region are S_2 =4(((49π)/3)−((49(√3))/4)) Consequently,the area of is shaded region equal to S_(squareABCD) −(S_1 +S_2 ) =14^2 −8(49−((49π)/6)−((49(√3))/4))−4(((49π)/3)−((49(√3))/4)) =3.49(√3)−196≈58.61

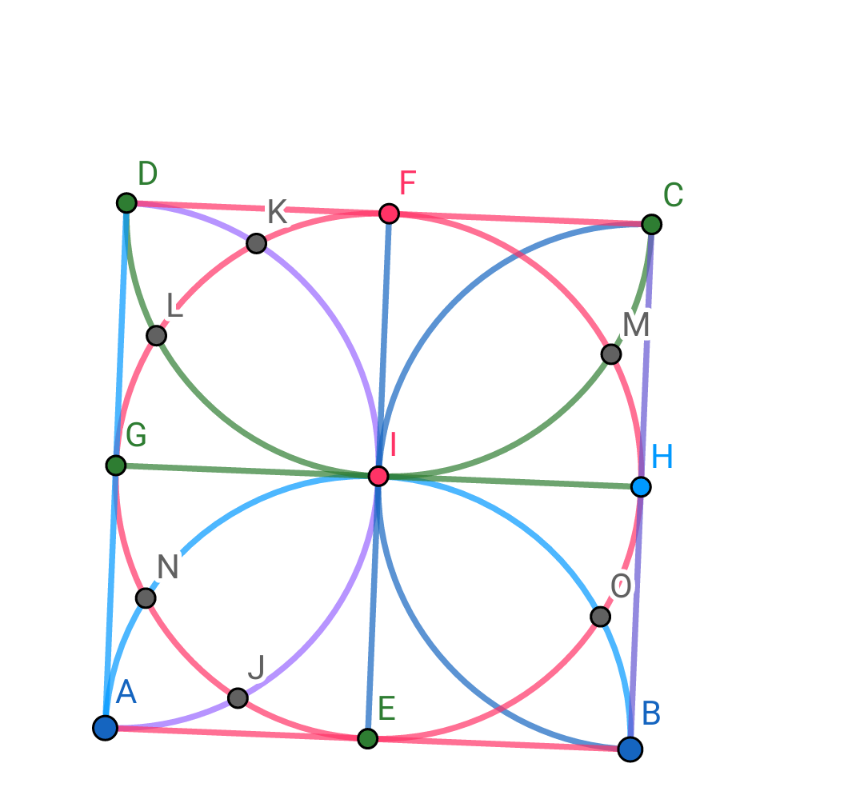
$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that} \\ $$$$\:\overset{\frown} {\mathrm{FK}}=\overset{\frown} {\mathrm{KL}}=\overset{\frown} {\mathrm{LG}}=\overset{\frown} {\mathrm{GN}}=\overset{\frown} {\mathrm{NJ}}=\overset{\frown} {\mathrm{JE}} \\ $$$$=\frac{\pi}{\mathrm{6}}\Rightarrow\widehat {\mathrm{FEK}}=\mathrm{15}° \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sector}\:\mathrm{IKF}\:\mathrm{is} \\ $$$$\mathrm{S}_{\mathrm{sectorIKF}} =\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{12}}=\frac{\mathrm{49}\pi}{\mathrm{12}}.\mathrm{The}\:\mathrm{are}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equalateral}\:\mathrm{triangle}\:\mathrm{IKG}\:\mathrm{is} \\ $$$$\mathrm{S}_{\Delta\mathrm{IKG}} =\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}.\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{curve} \\ $$$$\mathrm{triangle}\:\mathrm{DKF}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{S}_{\mathrm{DGIF}} −\mathrm{2}.\mathrm{S}_{\mathrm{sector}} \\ $$$$−\mathrm{S}_{\Delta\mathrm{IKG}} =\mathrm{49}−\frac{\mathrm{49}\pi}{\mathrm{6}}−\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{1}\right) \\ $$$$.\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sector} \\ $$$$\mathrm{ILM}\:\mathrm{is}\:\mathrm{S}_{\mathrm{sectorILM}} =\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{3}}=\frac{\mathrm{49}\pi}{\mathrm{3}}\left(\mathrm{since}\:\overset{\frown} {\mathrm{LFM}}=\mathrm{120}°\right) \\ $$$$\mathrm{S}_{\Delta\mathrm{ILM}} =\mathrm{S}_{\Delta\mathrm{IKG}} =\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}.\mathrm{Hence},\mathrm{the}\:\mathrm{area} \\ $$$$\mathrm{of}\:\mathrm{part}\:\mathrm{is}\:\mathrm{limited}\:\mathrm{by}\:\mathrm{the}\:\overset{\frown} {\mathrm{LIM}}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{arc}\:\overset{\frown} {\mathrm{LFM}}\:\mathrm{is}\:\mathrm{2}\left(\mathrm{S}_{\mathrm{sectorILM}} −\mathrm{S}_{\Delta\mathrm{ILM}} \right) \\ $$$$=\mathrm{2}\left(\frac{\mathrm{49}\pi}{\mathrm{3}}−\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{The}\:\mathrm{are}\:\mathrm{of}\:\mathrm{eight}\:\mathrm{curve}\:\mathrm{white}\:\mathrm{triangle}\:\mathrm{are} \\ $$$$\mathrm{S}_{\mathrm{1}} =\mathrm{8}\left(\mathrm{49}−\frac{\mathrm{49}\pi}{\mathrm{6}}−\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}\right)\left(\mathrm{3}\right).\mathrm{The}\:\mathrm{area}\:\mathrm{of}\:\mathrm{two}\: \\ $$$$\mathrm{big}\:\mathrm{white}\:\mathrm{region}\:\mathrm{are}\:\mathrm{S}_{\mathrm{2}} =\mathrm{4}\left(\frac{\mathrm{49}\pi}{\mathrm{3}}−\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$\mathrm{Consequently},\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{is}\:\mathrm{shaded}\: \\ $$$$\mathrm{region}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{S}_{\mathrm{squareABCD}} −\left(\mathrm{S}_{\mathrm{1}} +\mathrm{S}_{\mathrm{2}} \right) \\ $$$$=\mathrm{14}^{\mathrm{2}} −\mathrm{8}\left(\mathrm{49}−\frac{\mathrm{49}\pi}{\mathrm{6}}−\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}\right)−\mathrm{4}\left(\frac{\mathrm{49}\pi}{\mathrm{3}}−\frac{\mathrm{49}\sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$=\mathrm{3}.\mathrm{49}\sqrt{\mathrm{3}}−\mathrm{196}\approx\mathrm{58}.\mathrm{61} \\ $$

Commented by 1549442205PVT last updated on 12/Sep/20

Using Geogebra software.Drawing in tinkutara also did this thing

$$\mathrm{Using}\:\mathrm{Geogebra}\:\mathrm{software}.\mathrm{Drawing} \\ $$$$\mathrm{in}\:\mathrm{tinkutara}\:\mathrm{also}\:\mathrm{did}\:\:\mathrm{this}\:\mathrm{thing} \\ $$

Commented by Aina Samuel Temidayo last updated on 12/Sep/20

Ok. Thanks.

$$\mathrm{Ok}.\:\mathrm{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com