Question and Answers Forum

All Questions      Topic List

Logic Questions

Previous in All Question      Next in All Question      

Previous in Logic      Next in Logic      

Question Number 113211 by bemath last updated on 11/Sep/20

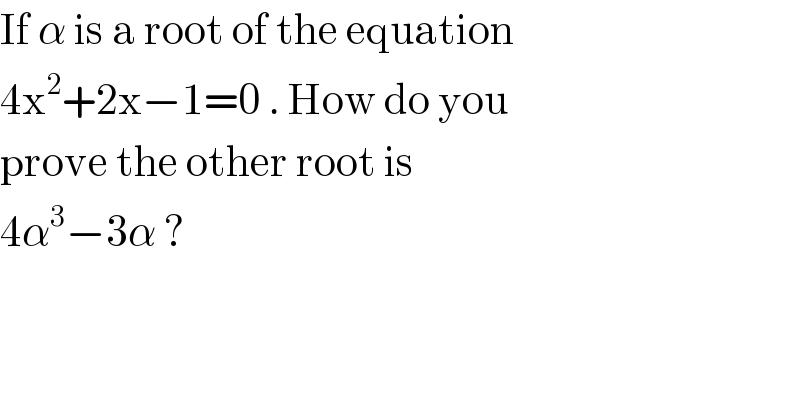
If α is a root of the equation 4x^2 +2x−1=0 . How do you prove the other root is 4α^3 −3α ?

Ifαisarootoftheequation4x2+2x−1=0.Howdoyouprovetheotherrootis4α3−3α?

Answered by 1549442205PVT last updated on 11/Sep/20

α is a root of the equation 4x^2 +2x−1=0 (1) ,so we have 4α^2 +2α−1=0 ⇒4α^3 =α(1−2α)=α−2α^2 .From that 4α^3 −3α=−2α^2 −2α.Replace into(1) we get 4(2α^2 +2α)^2 −2(2α^2 +2α)−1 =16(α^4 +2α^3 +α^2 )−4α^2 −4α−1 =16α^4 +32α^3 +12α^2 −4α−1 =(4α^2 +2α−1)^2 +16α^3 +16α^2 −2 =16α^3 +16α^2 −2=4α(4α^2 +2α−1) +8α^2 +4α−2=8α^2 +4α−2 =2(4α^2 +2α−1)=0 This show that 4α^3 −3α is also other root of the equation 4x^2 +2x−1=0(q.e.d)

αisarootoftheequation4x2+2x−1=0(1),sowehave4α2+2α−1=0⇒4α3=α(1−2α)=α−2α2.Fromthat4α3−3α=−2α2−2α.Replaceinto(1)weget4(2α2+2α)2−2(2α2+2α)−1=16(α4+2α3+α2)−4α2−4α−1=16α4+32α3+12α2−4α−1=(4α2+2α−1)2+16α3+16α2−2=16α3+16α2−2=4α(4α2+2α−1)+8α2+4α−2=8α2+4α−2=2(4α2+2α−1)=0Thisshowthat4α3−3αisalsootherrootoftheequation4x2+2x−1=0(q.e.d)

Answered by $@y@m last updated on 11/Sep/20

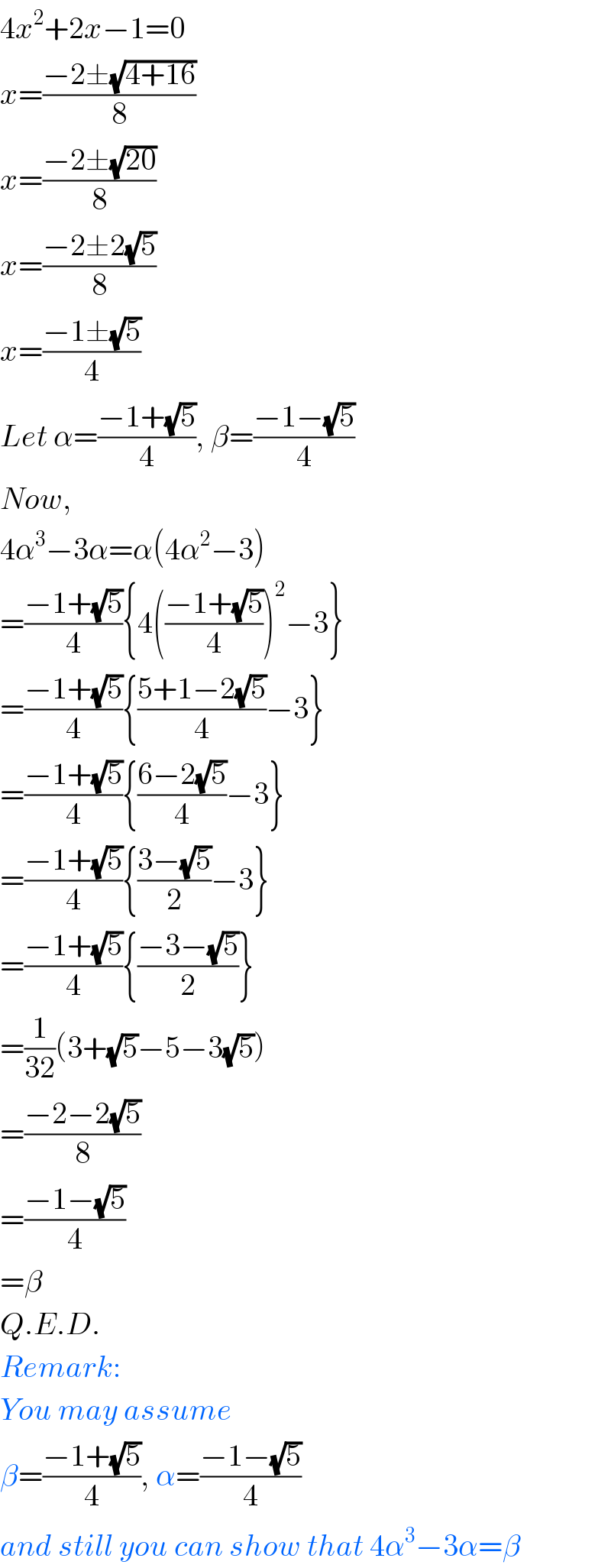
4x^2 +2x−1=0 x=((−2±(√(4+16)))/8) x=((−2±(√(20)))/8) x=((−2±2(√5))/8) x=((−1±(√5))/4) Let α=((−1+(√5))/4), β=((−1−(√5))/4) Now, 4α^3 −3α=α(4α^2 −3) =((−1+(√5))/4){4(((−1+(√5))/4))^2 −3} =((−1+(√5))/4){((5+1−2(√5))/4)−3} =((−1+(√5))/4){((6−2(√5))/4)−3} =((−1+(√5))/4){((3−(√5))/2)−3} =((−1+(√5))/4){((−3−(√5))/2)} =(1/(32))(3+(√5)−5−3(√5)) =((−2−2(√5))/8) =((−1−(√5))/4) =β Q.E.D. Remark: You may assume β=((−1+(√5))/4), α=((−1−(√5))/4) and still you can show that 4α^3 −3α=β

4x2+2x−1=0x=−2±4+168x=−2±208x=−2±258x=−1±54Letα=−1+54,β=−1−54Now,4α3−3α=α(4α2−3)=−1+54{4(−1+54)2−3}=−1+54{5+1−254−3}=−1+54{6−254−3}=−1+54{3−52−3}=−1+54{−3−52}=132(3+5−5−35)=−2−258=−1−54=βQ.E.D.Remark:Youmayassumeβ=−1+54,α=−1−54andstillyoucanshowthat4α3−3α=β

Commented by 1549442205PVT last updated on 12/Sep/20

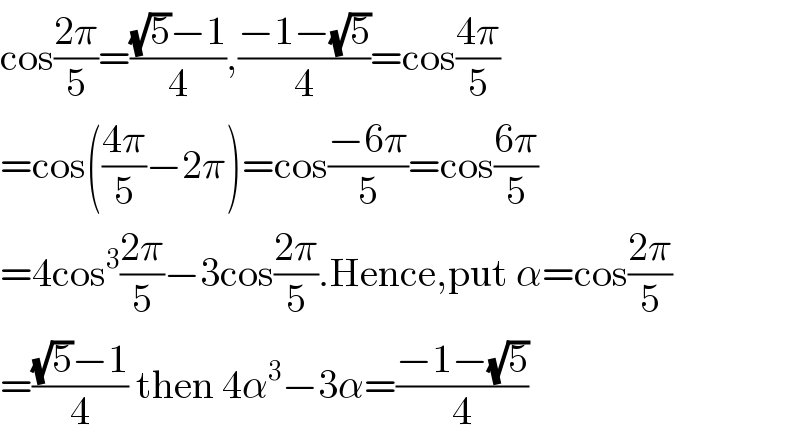
cos((2π)/5)=(((√5)−1)/4),((−1−(√5))/4)=cos((4π)/5) =cos(((4π)/5)−2π)=cos((−6π)/5)=cos((6π)/5) =4cos^3 ((2π)/5)−3cos((2π)/5).Hence,put α=cos((2π)/5) =(((√5)−1)/4) then 4α^3 −3α=((−1−(√5))/4)

cos2π5=5−14,−1−54=cos4π5=cos(4π5−2π)=cos−6π5=cos6π5=4cos32π5−3cos2π5.Hence,putα=cos2π5=5−14then4α3−3α=−1−54

Answered by Dwaipayan Shikari last updated on 11/Sep/20

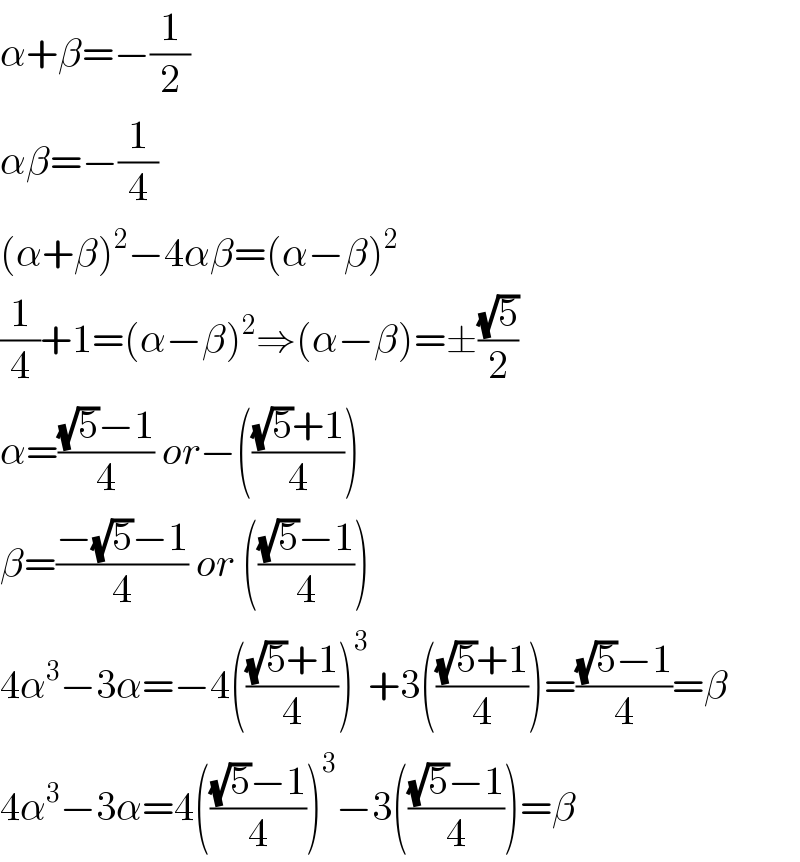
α+β=−(1/2) αβ=−(1/4) (α+β)^2 −4αβ=(α−β)^2 (1/4)+1=(α−β)^2 ⇒(α−β)=±((√5)/2) α=(((√5)−1)/4) or−((((√5)+1)/4)) β=((−(√5)−1)/4) or ((((√5)−1)/4)) 4α^3 −3α=−4((((√5)+1)/4))^3 +3((((√5)+1)/4))=(((√5)−1)/4)=β 4α^3 −3α=4((((√5)−1)/4))^3 −3((((√5)−1)/4))=β

α+β=−12αβ=−14(α+β)2−4αβ=(α−β)214+1=(α−β)2⇒(α−β)=±52α=5−14or−(5+14)β=−5−14or(5−14)4α3−3α=−4(5+14)3+3(5+14)=5−14=β4α3−3α=4(5−14)3−3(5−14)=β

Terms of Service

Privacy Policy

Contact: info@tinkutara.com