
Question Number 11321 by Joel576 last updated on 20/Mar/17
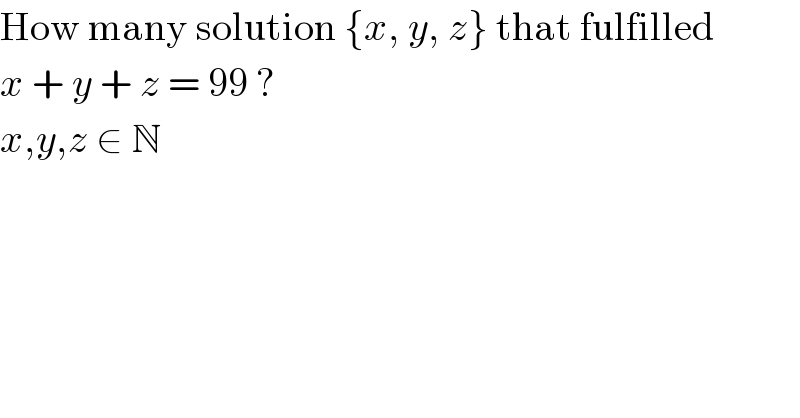
$$\mathrm{How}\:\mathrm{many}\:\mathrm{solution}\:\left\{{x},\:{y},\:{z}\right\}\:\mathrm{that}\:\mathrm{fulfilled} \\ $$$${x}\:+\:{y}\:+\:{z}\:=\:\mathrm{99}\:? \\ $$$${x},{y},{z}\:\in\:\mathbb{N} \\ $$
Commented by prakash jain last updated on 22/Mar/17

$$\mathrm{Please}\:\mathrm{have}\:\mathrm{a}\:\mathrm{look}\:\mathrm{at}\:\mathrm{stars}\:\mathrm{and}\:\mathrm{bars} \\ $$$$\mathrm{method}\:\mathrm{as}\:\mathrm{well}. \\ $$$$\mathrm{Suppose}\:{n}\:\mathrm{objects}\:\mathrm{are}\:\mathrm{to}\:\mathrm{be}\:\mathrm{divided} \\ $$$$\mathrm{in}\:{r}\:\mathrm{partitions}\:\mathrm{with}\:\mathrm{no}\:\mathrm{partition}\:\mathrm{become} \\ $$$$\mathrm{empty}. \\ $$$$\bigstar\bigstar\bigstar...\bigstar\:\left({n}\:\mathrm{stars}\:\mathrm{are}\:\mathrm{objects}\right) \\ $$$$\mathrm{to}\:\mathrm{divide}\:\mathrm{than}\:\mathrm{in}\:{r}\:\mathrm{partitions}\:\mathrm{we}\:\mathrm{put} \\ $$$${r}−\mathrm{1}\:\mathrm{bars}\:\mathrm{in}\:\mathrm{some}\:\mathrm{of}\:\mathrm{the}\:{n}−\mathrm{1}\:\mathrm{space} \\ $$$$\mathrm{between}\:\mathrm{stars}. \\ $$$$\mathrm{examples} \\ $$$$\mathrm{5}\:\mathrm{objects}\:\mathrm{in}\:\mathrm{3}\:\mathrm{partions} \\ $$$$\bigstar\bigstar\mid\bigstar\mid\bigstar\bigstar \\ $$$$\bigstar\mid\bigstar\bigstar\bigstar\mid\bigstar \\ $$$$\mathrm{basically}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{using}\:\left({r}−\mathrm{1}\right)\:\mathrm{positions} \\ $$$$\mathrm{from}\:\left({n}−\mathrm{1}\right)\:\mathrm{choices}. \\ $$$$\mathrm{Or}:\:^{{n}−\mathrm{1}} {C}_{{r}−\mathrm{1}} \\ $$$${x}+{y}+{z}={n},\:{x},{y},{z}\in\mathbb{N} \\ $$$${can}\:{be}\:{taken}\:{as}\:{divided}\:{n}\:{objects}\:{in}\:\mathrm{3} \\ $$$${partitions},\:{number}\:{of}\:{stars}\:{in}\:{each} \\ $$$${partitions}\:{as}\:{value}\:{of}\:{x},{y},{z}\:{ans}\:{bars} \\ $$$${are}\:{plus}\:{sign}. \\ $$$$\mathrm{If}\:\mathrm{zero}\:\mathrm{are}\:\mathrm{allowed}\:\mathrm{in}\:\mathrm{partition}\:\mathrm{then}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{is}\:\:^{{n}+{r}−\mathrm{1}} {C}_{{n}} \\ $$
Commented by mrW1 last updated on 22/Mar/17
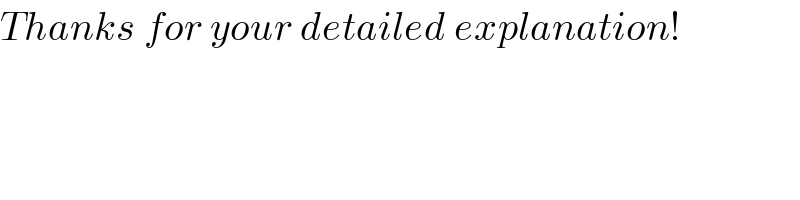
$${Thanks}\:{for}\:{your}\:{detailed}\:{explanation}! \\ $$
Answered by mrW1 last updated on 21/Mar/17

$${Generally}\:{the}\:{equation}\:{x}+{y}={n}\: \\ $$$${with}\:{x},\:{y},\:{n}\in\mathbb{N}\:{and}\:{n}\geqslant\mathrm{2} \\ $$$${has}\:{following}\:{solutions}\:{for}\:{x}/{y}: \\ $$$$\mathrm{1}/{n}−\mathrm{1} \\ $$$$\mathrm{2}/{n}−\mathrm{2} \\ $$$$\mathrm{3}/{n}−\mathrm{3} \\ $$$$... \\ $$$${n}−\mathrm{1}/\mathrm{1} \\ $$$$\Rightarrow{total}\:{number}\:{of}\:{solutions}\:=\:{n}−\mathrm{1}. \\ $$$$ \\ $$$${The}\:{equation}\:{x}+{y}+{z}=\mathrm{99}\:{has}\:{following} \\ $$$${number}\:{of}\:{solutions}: \\ $$$${z}=\mathrm{97}\Rightarrow{x}+{y}=\mathrm{2}\Rightarrow{no}.\:{of}\:{sol}.=\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$$${z}=\mathrm{96}\Rightarrow{x}+{y}=\mathrm{3}\Rightarrow{no}.\:{of}\:{sol}.=\mathrm{3}−\mathrm{1}=\mathrm{2} \\ $$$${z}=\mathrm{95}\Rightarrow{x}+{y}=\mathrm{4}\Rightarrow{no}.\:{of}\:{sol}.=\mathrm{4}−\mathrm{1}=\mathrm{3} \\ $$$$...... \\ $$$${z}=\mathrm{2}\Rightarrow{x}+{y}=\mathrm{97}\Rightarrow{no}.\:{of}\:{sol}.=\mathrm{97}−\mathrm{1}=\mathrm{96} \\ $$$${z}=\mathrm{1}\Rightarrow{x}+{y}=\mathrm{98}\Rightarrow{no}.\:{of}\:{sol}.=\mathrm{98}−\mathrm{1}=\mathrm{97} \\ $$$$ \\ $$$$\Rightarrow{total}\:{no}.\:{of}\:{sol}.=\frac{\mathrm{1}+\mathrm{97}}{\mathrm{2}}×\mathrm{97}=\mathrm{4753} \\ $$$$ \\ $$$${In}\:{general}\:{x}+{y}+{z}={n}\:\left({n}\geqslant\mathrm{3}\right)\:{has} \\ $$$$\frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}} \\ $$$${solutions}. \\ $$$$ \\ $$$${In}\:{general}\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} ={n}\:\left({n}\geqslant\mathrm{4}\right)\:{has} \\ $$$$\frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\left({n}−\mathrm{3}\right)}{\mathrm{6}} \\ $$$${solutions}. \\ $$$$ \\ $$$${In}\:{general}\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +\centerdot\centerdot\centerdot+{x}_{{k}} ={n}\:\left({n}\geqslant{k}\right)\:{has} \\ $$$$\:^{{n}−\mathrm{1}} {C}_{{k}−\mathrm{1}} =\frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\centerdot\centerdot\centerdot\left({n}−{k}+\mathrm{1}\right)}{\left({k}−\mathrm{1}\right)!} \\ $$$${solutions}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Mar/17

$${thank}\:{you}\:{dear}\:{mrW}\mathrm{1}.{your}\:{answers} \\ $$$${are}\:{so}\:{beautiful}\:{and}\:{perfect}. \\ $$
Answered by ajfour last updated on 20/Mar/17

$$\:^{\mathrm{98}} \mathrm{C}_{\mathrm{2}} \\ $$
Commented by ajfour last updated on 20/Mar/17
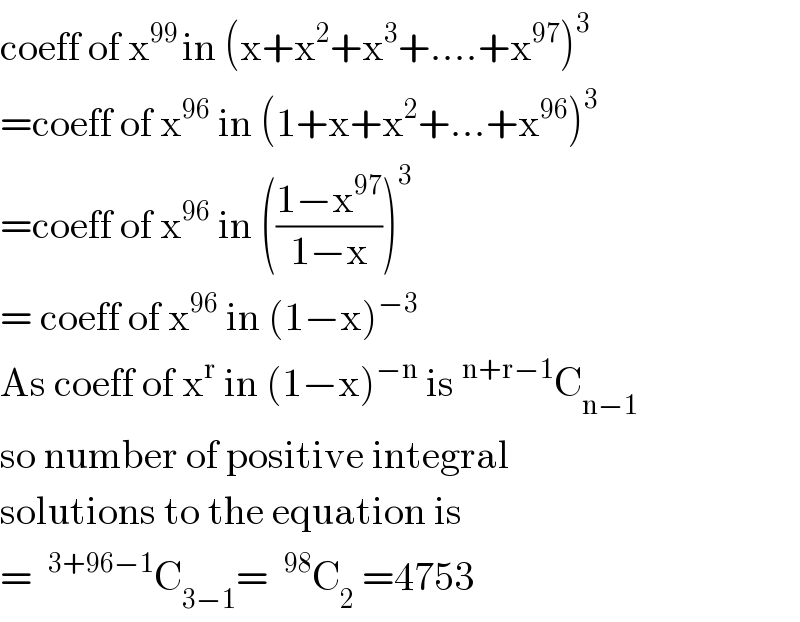
$$\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{99}\:} \mathrm{in}\:\left(\mathrm{x}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{3}} +....+\mathrm{x}^{\mathrm{97}} \right)^{\mathrm{3}} \\ $$$$=\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{96}} \:\mathrm{in}\:\left(\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} +...+\mathrm{x}^{\mathrm{96}} \right)^{\mathrm{3}} \\ $$$$=\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{96}} \:\mathrm{in}\:\left(\frac{\mathrm{1}−\mathrm{x}^{\mathrm{97}} }{\mathrm{1}−\mathrm{x}}\right)^{\mathrm{3}} \\ $$$$=\:\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{96}} \:\mathrm{in}\:\left(\mathrm{1}−\mathrm{x}\right)^{−\mathrm{3}} \\ $$$$\mathrm{As}\:\mathrm{coeff}\:\mathrm{of}\:\mathrm{x}^{\mathrm{r}} \:\mathrm{in}\:\left(\mathrm{1}−\mathrm{x}\right)^{−\mathrm{n}} \:\mathrm{is}\:^{\mathrm{n}+\mathrm{r}−\mathrm{1}} \mathrm{C}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{so}\:\mathrm{number}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integral} \\ $$$$\mathrm{solutions}\:\mathrm{to}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is} \\ $$$$=\:\:^{\mathrm{3}+\mathrm{96}−\mathrm{1}} \mathrm{C}_{\mathrm{3}−\mathrm{1}} =\:\:^{\mathrm{98}} \mathrm{C}_{\mathrm{2}} \:=\mathrm{4753} \\ $$
