
Question Number 1130 by 123456 last updated on 22/Jun/15
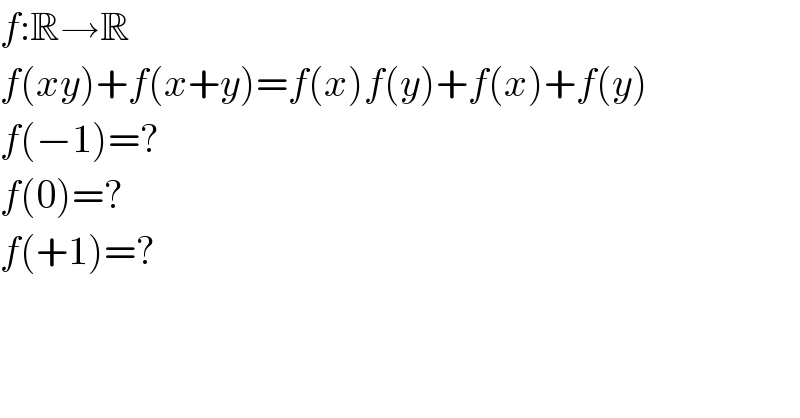
$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({xy}\right)+{f}\left({x}+{y}\right)={f}\left({x}\right){f}\left({y}\right)+{f}\left({x}\right)+{f}\left({y}\right) \\ $$$${f}\left(−\mathrm{1}\right)=? \\ $$$${f}\left(\mathrm{0}\right)=? \\ $$$${f}\left(+\mathrm{1}\right)=? \\ $$
Answered by prakash jain last updated on 23/Jun/15
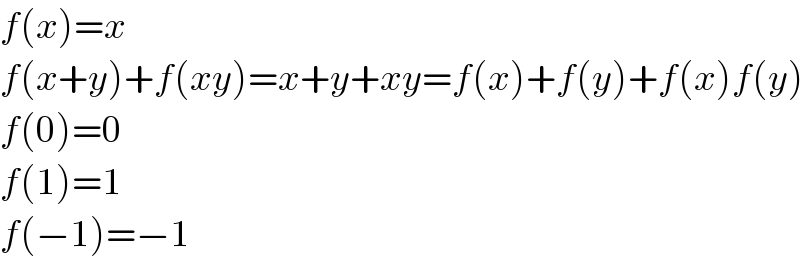
$${f}\left({x}\right)={x} \\ $$$${f}\left({x}+{y}\right)+{f}\left({xy}\right)={x}+{y}+{xy}={f}\left({x}\right)+{f}\left({y}\right)+{f}\left({x}\right){f}\left({y}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${f}\left(−\mathrm{1}\right)=−\mathrm{1} \\ $$
Commented by Rasheed Soomro last updated on 15/Jul/15
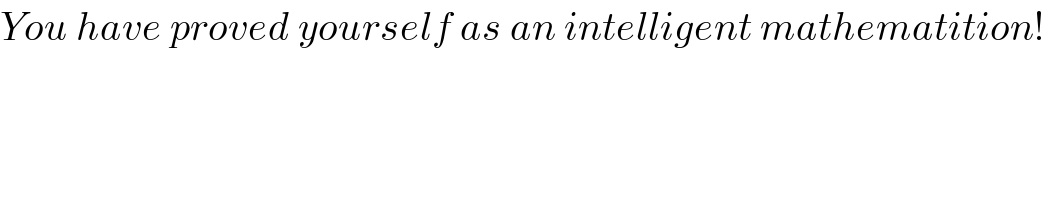
$${You}\:{have}\:{proved}\:{yourself}\:{as}\:{an}\:{intelligent}\:{mathematition}! \\ $$$$ \\ $$
