
Question Number 112885 by malwan last updated on 10/Sep/20
Commented by malwan last updated on 10/Sep/20
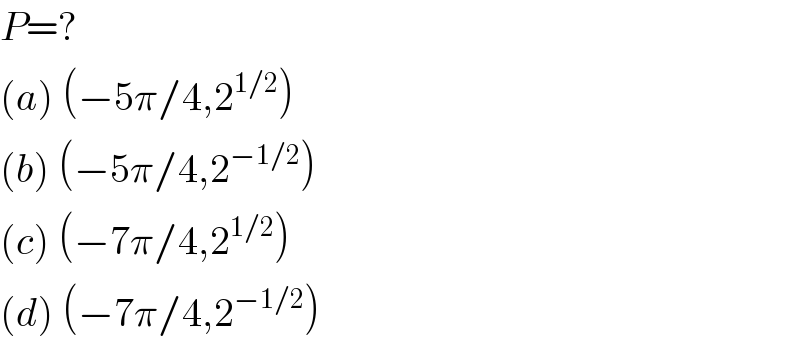
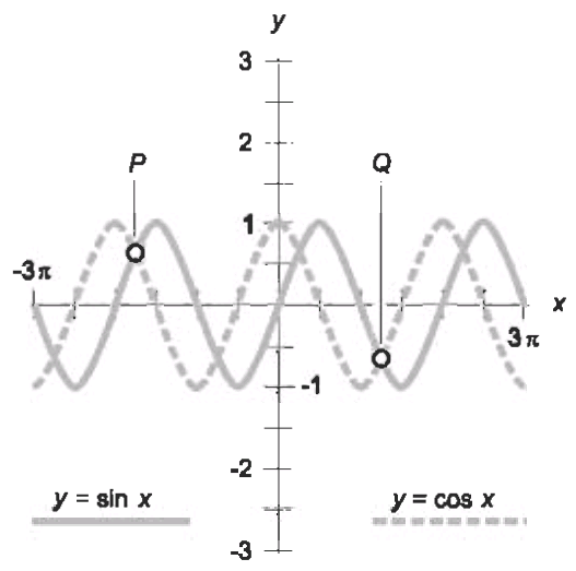
$${P}=? \\ $$$$\left({a}\right)\:\left(−\mathrm{5}\pi/\mathrm{4},\mathrm{2}^{\mathrm{1}/\mathrm{2}} \right) \\ $$$$\left({b}\right)\:\left(−\mathrm{5}\pi/\mathrm{4},\mathrm{2}^{−\mathrm{1}/\mathrm{2}} \right) \\ $$$$\left({c}\right)\:\left(−\mathrm{7}\pi/\mathrm{4},\mathrm{2}^{\mathrm{1}/\mathrm{2}} \right) \\ $$$$\left({d}\right)\:\left(−\mathrm{7}\pi/\mathrm{4},\mathrm{2}^{−\mathrm{1}/\mathrm{2}} \right) \\ $$
Commented by malwan last updated on 10/Sep/20
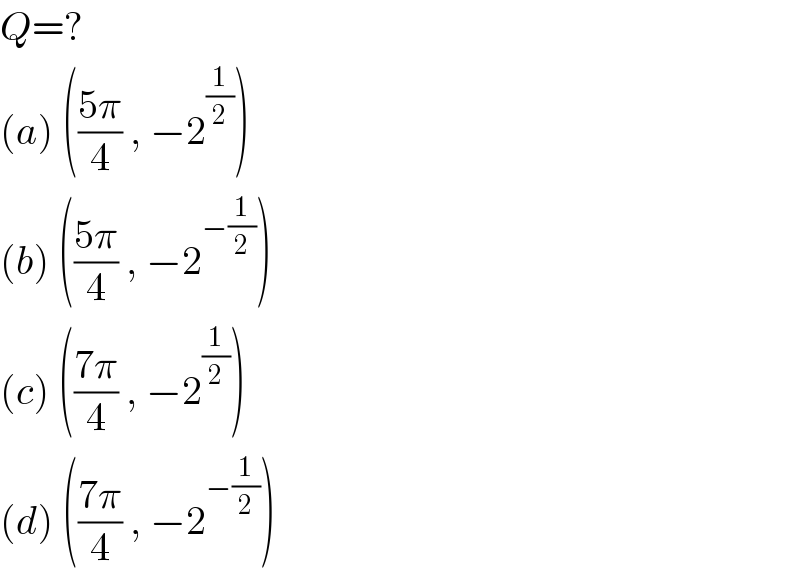
$${Q}=? \\ $$$$\left({a}\right)\:\left(\frac{\mathrm{5}\pi}{\mathrm{4}}\:,\:−\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$$$\left({b}\right)\:\left(\frac{\mathrm{5}\pi}{\mathrm{4}}\:,\:−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$$$\left({c}\right)\:\left(\frac{\mathrm{7}\pi}{\mathrm{4}}\:,\:−\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$$$\left({d}\right)\:\left(\frac{\mathrm{7}\pi}{\mathrm{4}}\:,\:−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$
Commented by Aziztisffola last updated on 10/Sep/20
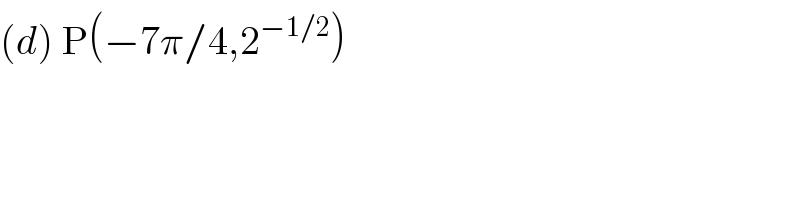
$$\left({d}\right)\:\mathrm{P}\left(−\mathrm{7}\pi/\mathrm{4},\mathrm{2}^{−\mathrm{1}/\mathrm{2}} \right) \\ $$
Commented by Aziztisffola last updated on 10/Sep/20

$$\left({b}\right)\:\mathrm{Q}\left(\frac{\mathrm{5}\pi}{\mathrm{4}}\:,\:−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right) \\ $$
Commented by malwan last updated on 10/Sep/20

$${thank}\:{you} \\ $$
Commented by malwan last updated on 10/Sep/20
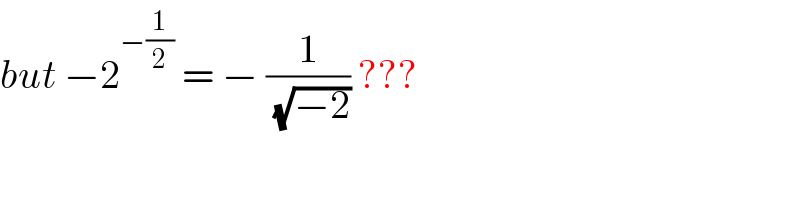
$${but}\:−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:−\:\frac{\mathrm{1}}{\:\sqrt{−\mathrm{2}}}\:??? \\ $$
Commented by Aziztisffola last updated on 10/Sep/20
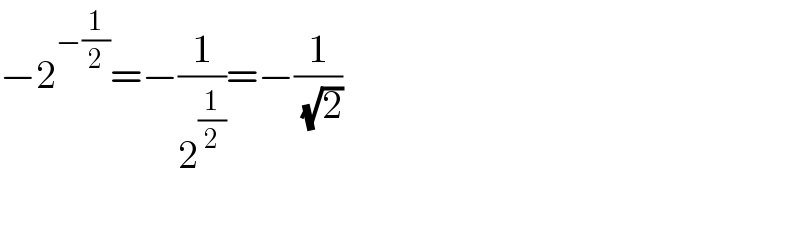
$$−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} =−\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} }=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$
Commented by malwan last updated on 10/Sep/20
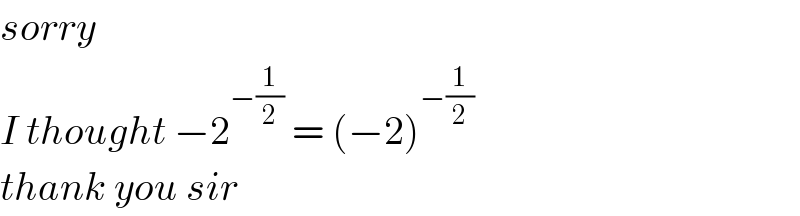
$${sorry} \\ $$$${I}\:{thought}\:−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\left(−\mathrm{2}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${thank}\:{you}\:{sir} \\ $$
Commented by Aziztisffola last updated on 10/Sep/20
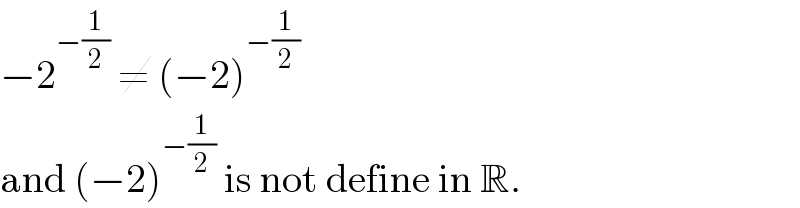
$$−\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\neq\:\left(−\mathrm{2}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{and}\:\left(−\mathrm{2}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{define}\:\mathrm{in}\:\mathbb{R}. \\ $$
