
Question Number 112874 by sandy_delta last updated on 10/Sep/20
![y=sec{sec[tan(tan(sin 4x^2 ))]} (dy/dx) = ?](Q112874.png)
$$\mathrm{y}=\mathrm{sec}\left\{\mathrm{sec}\left[\mathrm{tan}\left(\mathrm{tan}\left(\mathrm{sin}\:\mathrm{4x}^{\mathrm{2}} \right)\right)\right]\right\} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:? \\ $$
Commented by MJS_new last updated on 10/Sep/20
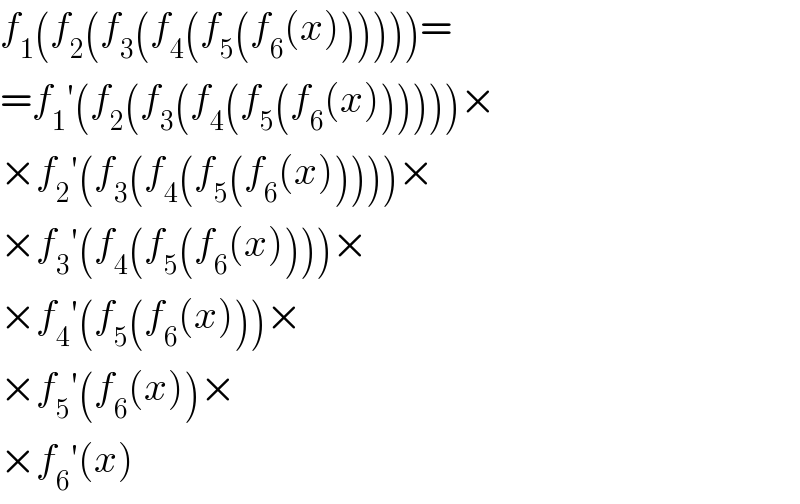
$${f}_{\mathrm{1}} \left({f}_{\mathrm{2}} \left({f}_{\mathrm{3}} \left({f}_{\mathrm{4}} \left({f}_{\mathrm{5}} \left({f}_{\mathrm{6}} \left({x}\right)\right)\right)\right)\right)\right)= \\ $$$$={f}_{\mathrm{1}} '\left({f}_{\mathrm{2}} \left({f}_{\mathrm{3}} \left({f}_{\mathrm{4}} \left({f}_{\mathrm{5}} \left({f}_{\mathrm{6}} \left({x}\right)\right)\right)\right)\right)\right)× \\ $$$$×{f}_{\mathrm{2}} '\left({f}_{\mathrm{3}} \left({f}_{\mathrm{4}} \left({f}_{\mathrm{5}} \left({f}_{\mathrm{6}} \left({x}\right)\right)\right)\right)\right)× \\ $$$$×{f}_{\mathrm{3}} '\left({f}_{\mathrm{4}} \left({f}_{\mathrm{5}} \left({f}_{\mathrm{6}} \left({x}\right)\right)\right)\right)× \\ $$$$×{f}_{\mathrm{4}} '\left({f}_{\mathrm{5}} \left({f}_{\mathrm{6}} \left({x}\right)\right)\right)× \\ $$$$×{f}_{\mathrm{5}} '\left({f}_{\mathrm{6}} \left({x}\right)\right)× \\ $$$$×{f}_{\mathrm{6}} '\left({x}\right) \\ $$
Commented by sandy_delta last updated on 10/Sep/20
$$\mathrm{thanks}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$
Answered by bobhans last updated on 10/Sep/20
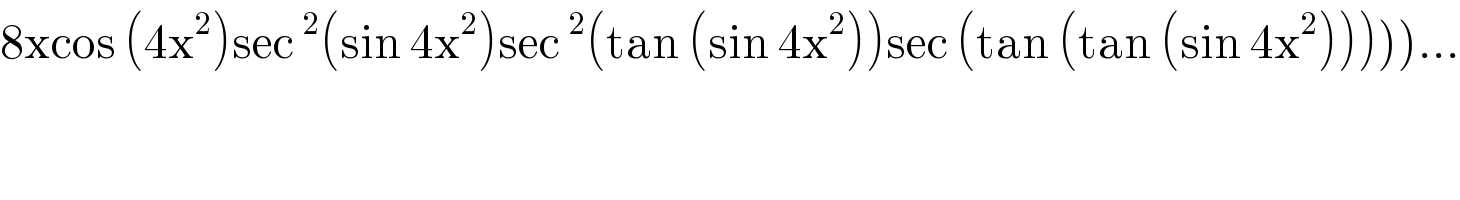
$$\left.\mathrm{8}\left.\mathrm{xcos}\:\left(\mathrm{4x}^{\mathrm{2}} \right)\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{sin}\:\mathrm{4x}^{\mathrm{2}} \right)\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{tan}\:\left(\mathrm{sin}\:\mathrm{4x}^{\mathrm{2}} \right)\right)\mathrm{sec}\:\left(\mathrm{tan}\:\left(\mathrm{tan}\:\left(\mathrm{sin}\:\mathrm{4x}^{\mathrm{2}} \right)\right)\right)\right)\right)... \\ $$
Commented by sandy_delta last updated on 10/Sep/20
$$\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{Sir}? \\ $$
