
Question Number 11272 by chux last updated on 18/Mar/17
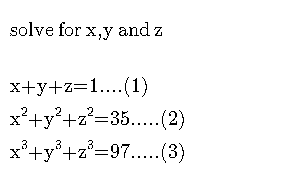
Answered by mrW1 last updated on 18/Mar/17
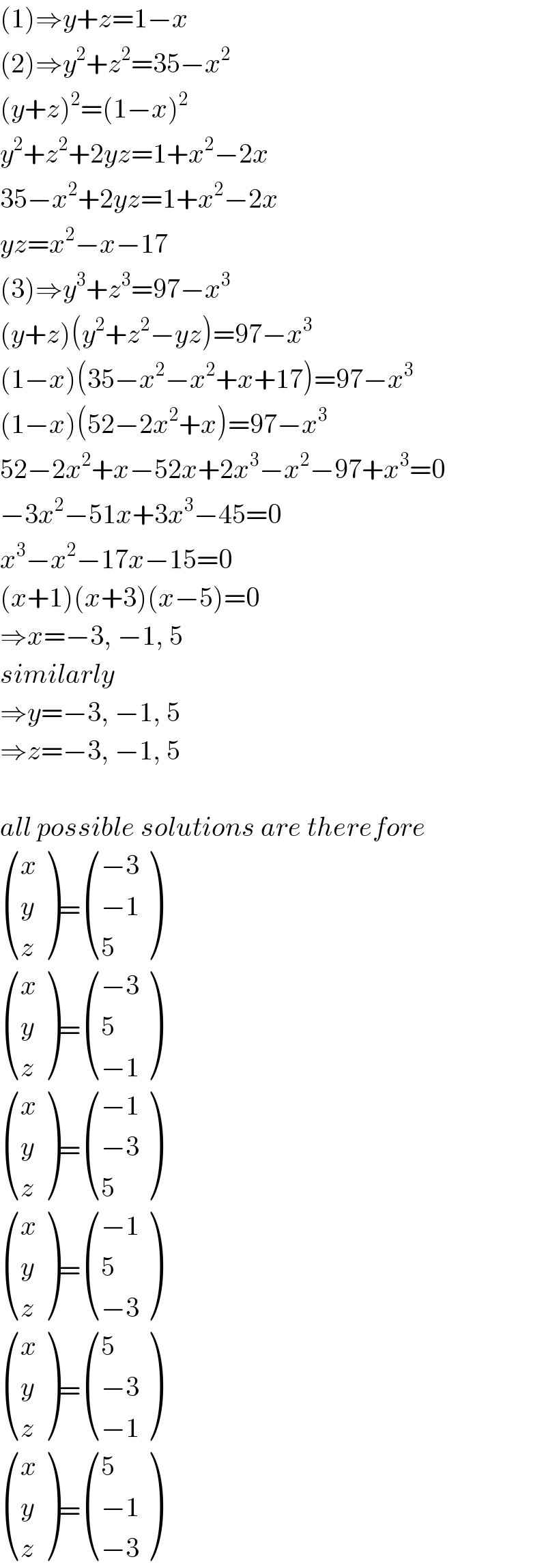
$$\left(\mathrm{1}\right)\Rightarrow{y}+{z}=\mathrm{1}−{x} \\ $$$$\left(\mathrm{2}\right)\Rightarrow{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{35}−{x}^{\mathrm{2}} \\ $$$$\left({y}+{z}\right)^{\mathrm{2}} =\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{yz}=\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x} \\ $$$$\mathrm{35}−{x}^{\mathrm{2}} +\mathrm{2}{yz}=\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{x} \\ $$$${yz}={x}^{\mathrm{2}} −{x}−\mathrm{17} \\ $$$$\left(\mathrm{3}\right)\Rightarrow{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{97}−{x}^{\mathrm{3}} \\ $$$$\left({y}+{z}\right)\left({y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{yz}\right)=\mathrm{97}−{x}^{\mathrm{3}} \\ $$$$\left(\mathrm{1}−{x}\right)\left(\mathrm{35}−{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +{x}+\mathrm{17}\right)=\mathrm{97}−{x}^{\mathrm{3}} \\ $$$$\left(\mathrm{1}−{x}\right)\left(\mathrm{52}−\mathrm{2}{x}^{\mathrm{2}} +{x}\right)=\mathrm{97}−{x}^{\mathrm{3}} \\ $$$$\mathrm{52}−\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{52}{x}+\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{97}+{x}^{\mathrm{3}} =\mathrm{0} \\ $$$$−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{51}{x}+\mathrm{3}{x}^{\mathrm{3}} −\mathrm{45}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{17}{x}−\mathrm{15}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({x}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{3},\:−\mathrm{1},\:\mathrm{5} \\ $$$${similarly} \\ $$$$\Rightarrow{y}=−\mathrm{3},\:−\mathrm{1},\:\mathrm{5} \\ $$$$\Rightarrow{z}=−\mathrm{3},\:−\mathrm{1},\:\mathrm{5} \\ $$$$ \\ $$$${all}\:{possible}\:{solutions}\:{are}\:{therefore} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{−\mathrm{3}}\\{−\mathrm{1}}\\{\mathrm{5}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{−\mathrm{3}}\\{\mathrm{5}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{−\mathrm{1}}\\{−\mathrm{3}}\\{\mathrm{5}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{5}}\\{−\mathrm{3}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{\mathrm{5}}\\{−\mathrm{3}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\\{{z}}\end{pmatrix}=\begin{pmatrix}{\mathrm{5}}\\{−\mathrm{1}}\\{−\mathrm{3}}\end{pmatrix} \\ $$
Commented by chux last updated on 19/Mar/17
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:....\mathrm{thanx}\:\mathrm{alot}. \\ $$
