
Previous in Relation and Functions Next in Relation and Functions
Question Number 112681 by bemath last updated on 09/Sep/20
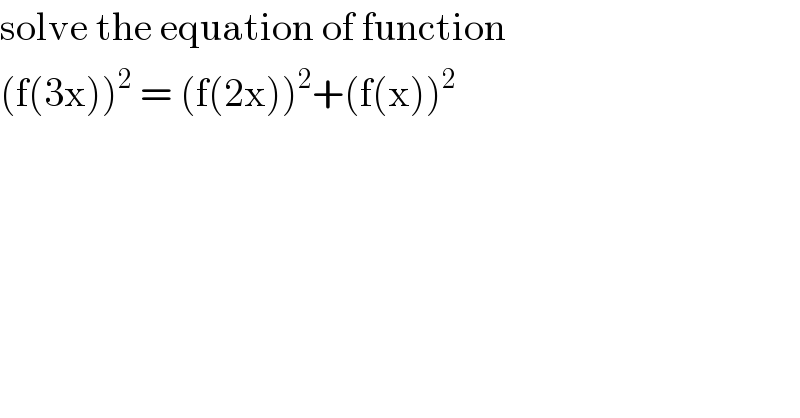
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{function}\: \\ $$$$\left(\mathrm{f}\left(\mathrm{3x}\right)\right)^{\mathrm{2}} \:=\:\left(\mathrm{f}\left(\mathrm{2x}\right)\right)^{\mathrm{2}} +\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{2}} \\ $$
Answered by bobhans last updated on 09/Sep/20
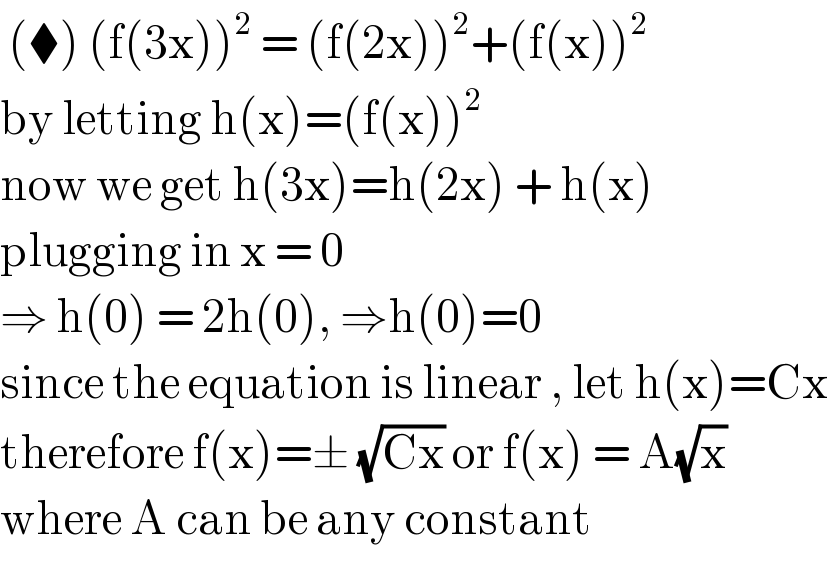
$$\:\left(\blacklozenge\right)\:\left(\mathrm{f}\left(\mathrm{3x}\right)\right)^{\mathrm{2}} \:=\:\left(\mathrm{f}\left(\mathrm{2x}\right)\right)^{\mathrm{2}} +\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{by}\:\mathrm{letting}\:\mathrm{h}\left(\mathrm{x}\right)=\left(\mathrm{f}\left(\mathrm{x}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{get}\:\mathrm{h}\left(\mathrm{3x}\right)=\mathrm{h}\left(\mathrm{2x}\right)\:+\:\mathrm{h}\left(\mathrm{x}\right) \\ $$$$\mathrm{plugging}\:\mathrm{in}\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{h}\left(\mathrm{0}\right)\:=\:\mathrm{2h}\left(\mathrm{0}\right),\:\Rightarrow\mathrm{h}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{since}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{linear}\:,\:\mathrm{let}\:\mathrm{h}\left(\mathrm{x}\right)=\mathrm{Cx} \\ $$$$\mathrm{therefore}\:\mathrm{f}\left(\mathrm{x}\right)=\pm\:\sqrt{\mathrm{Cx}}\:\mathrm{or}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{A}\sqrt{\mathrm{x}} \\ $$$$\mathrm{where}\:\mathrm{A}\:\mathrm{can}\:\mathrm{be}\:\mathrm{any}\:\mathrm{constant} \\ $$
