
Question Number 112320 by mohammad17 last updated on 07/Sep/20
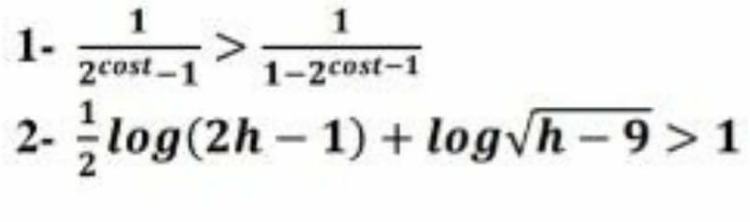
Commented by mohammad17 last updated on 07/Sep/20
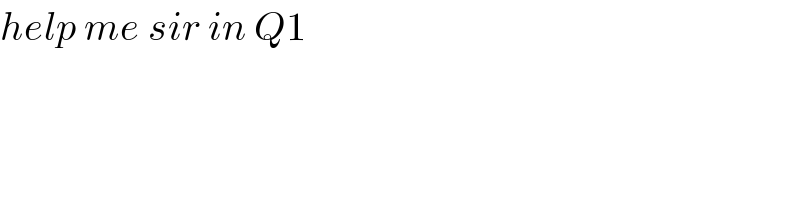
$${help}\:{me}\:{sir}\:{in}\:{Q}\mathrm{1} \\ $$
Answered by john santu last updated on 07/Sep/20
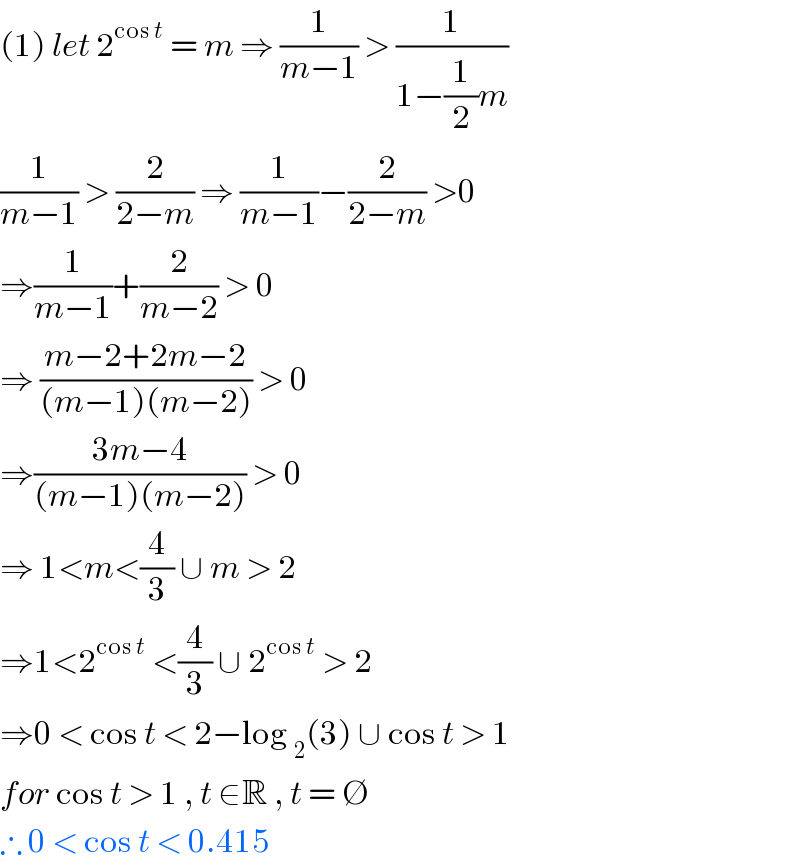
$$\left(\mathrm{1}\right)\:{let}\:\mathrm{2}^{\mathrm{cos}\:{t}} \:=\:{m}\:\Rightarrow\:\frac{\mathrm{1}}{{m}−\mathrm{1}}\:>\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{m}} \\ $$$$\frac{\mathrm{1}}{{m}−\mathrm{1}}\:>\:\frac{\mathrm{2}}{\mathrm{2}−{m}}\:\Rightarrow\:\frac{\mathrm{1}}{{m}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{2}−{m}}\:>\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{m}−\mathrm{1}}+\frac{\mathrm{2}}{{m}−\mathrm{2}}\:>\:\mathrm{0} \\ $$$$\Rightarrow\:\frac{{m}−\mathrm{2}+\mathrm{2}{m}−\mathrm{2}}{\left({m}−\mathrm{1}\right)\left({m}−\mathrm{2}\right)}\:>\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{3}{m}−\mathrm{4}}{\left({m}−\mathrm{1}\right)\left({m}−\mathrm{2}\right)}\:>\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{1}<{m}<\frac{\mathrm{4}}{\mathrm{3}}\:\cup\:{m}\:>\:\mathrm{2} \\ $$$$\Rightarrow\mathrm{1}<\mathrm{2}^{\mathrm{cos}\:{t}} \:<\frac{\mathrm{4}}{\mathrm{3}}\:\cup\:\mathrm{2}^{\mathrm{cos}\:{t}} \:>\:\mathrm{2} \\ $$$$\Rightarrow\mathrm{0}\:<\:\mathrm{cos}\:{t}\:<\:\mathrm{2}−\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}\right)\:\cup\:\mathrm{cos}\:{t}\:>\:\mathrm{1}\: \\ $$$${for}\:\mathrm{cos}\:{t}\:>\:\mathrm{1}\:,\:{t}\:\in\mathbb{R}\:,\:{t}\:=\:\varnothing \\ $$$$\therefore\:\mathrm{0}\:<\:\mathrm{cos}\:{t}\:<\:\mathrm{0}.\mathrm{415} \\ $$
Commented by mohammad17 last updated on 07/Sep/20

$${thank}\:{you}\:{sir} \\ $$
Answered by 1549442205PVT last updated on 08/Sep/20

$$\mathrm{Put}\:\mathrm{2}^{\mathrm{cost}} =\mathrm{x}.\mathrm{Then}\:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}>\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}>\frac{\mathrm{2}}{\mathrm{2}−\mathrm{x}}\Leftrightarrow\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{2}−\mathrm{x}}>\mathrm{0} \\ $$$$\frac{\mathrm{2}−\mathrm{x}−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{2}−\mathrm{x}\right)}>\mathrm{0}\Leftrightarrow\frac{\mathrm{4}−\mathrm{3x}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{2}−\mathrm{x}\right)}>\mathrm{0} \\ $$$$\Leftrightarrow\frac{\mathrm{3x}−\mathrm{4}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)}>\mathrm{0}\Leftrightarrow\frac{\mathrm{x}−\mathrm{4}/\mathrm{3}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)}>\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}\in\left(\mathrm{1};\frac{\mathrm{4}}{\mathrm{3}}\right)\cup\left(\mathrm{2};+\infty\right) \\ $$$$\left.\boldsymbol{{a}}\right)\boldsymbol{{x}}\in\left(\mathrm{1},\frac{ }{ }\right)\Leftrightarrow\mathrm{1}< ^{\boldsymbol{{cost}}} <\frac{ }{ }\: \\ $$$$\:\Leftrightarrow\mathrm{0}<\boldsymbol{\mathrm{cost}}<\frac{\boldsymbol{\mathrm{ln}}\left(\mathrm{4}/\mathrm{3}\right)}{\boldsymbol{\mathrm{ln}}\mathrm{2}}\approx\mathrm{0}.\mathrm{4150}=\boldsymbol{\mathrm{cos}}\mathrm{65}°\mathrm{29}' \\ $$$$\Leftrightarrow\mathrm{t}\in\left(−\mathrm{90}°+\mathrm{k360}°;−\mathrm{65}°\mathrm{28}'+\mathrm{k360}\right)\cup\left(\mathrm{65}°\mathrm{28}'+\mathrm{k360}°;\mathrm{90}°+\mathrm{k360}\right) \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\boldsymbol{\mathrm{x}}\in\left(\mathrm{2};+\infty\right)\Leftrightarrow\mathrm{2}^{\boldsymbol{\mathrm{cost}}} >\mathrm{2}\Leftrightarrow\boldsymbol{\mathrm{cost}}>\mathrm{1} \\ $$$$\boldsymbol{\mathrm{inequality}}\:\boldsymbol{\mathrm{has}}\:\boldsymbol{\mathrm{no}}\:\boldsymbol{\mathrm{roots}}\: \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{inequality}}\:\boldsymbol{\mathrm{has}}\:\boldsymbol{\mathrm{roots}}\:\boldsymbol{\mathrm{are}}: \\ $$$$\boldsymbol{\mathrm{t}}\in\left(−\mathrm{90}°+\boldsymbol{\mathrm{k}}\mathrm{360}°;−\mathrm{65}°\mathrm{28}'+\boldsymbol{\mathrm{k}}\mathrm{360}\right)\cup \\ $$$$\left(\mathrm{65}°\mathrm{28}'+\boldsymbol{\mathrm{k}}\mathrm{360}°;\mathrm{90}°+\boldsymbol{\mathrm{k}}\mathrm{360}°\right) \\ $$
