
Question Number 112169 by bemath last updated on 06/Sep/20
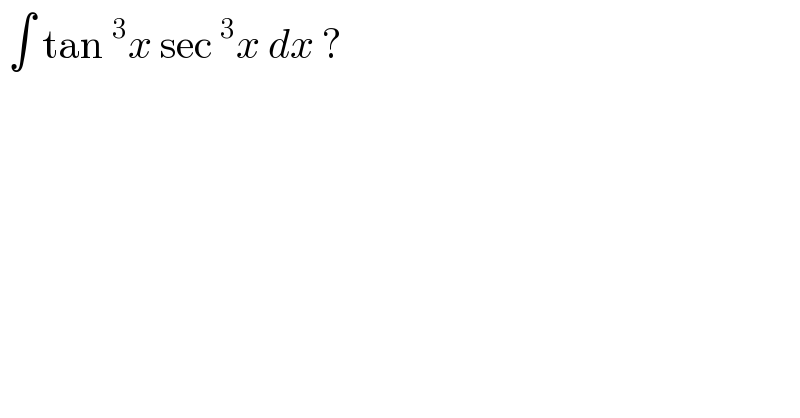
$$\:\int\:\mathrm{tan}\:^{\mathrm{3}} {x}\:\mathrm{sec}\:^{\mathrm{3}} {x}\:{dx}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 06/Sep/20
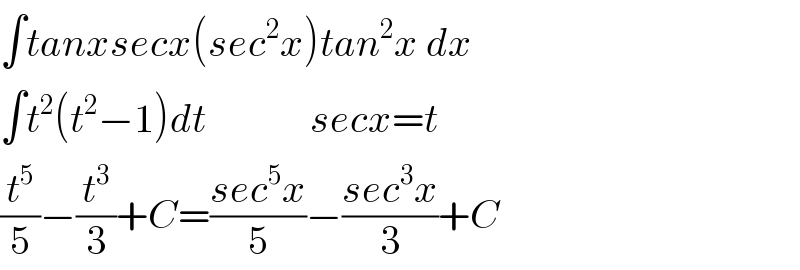
$$\int{tanxsecx}\left({sec}^{\mathrm{2}} {x}\right){tan}^{\mathrm{2}} {x}\:{dx} \\ $$$$\int{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right){dt}\:\:\:\:\:\:\:\:\:\:\:\:\:{secx}={t} \\ $$$$\frac{{t}^{\mathrm{5}} }{\mathrm{5}}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+{C}=\frac{{sec}^{\mathrm{5}} {x}}{\mathrm{5}}−\frac{{sec}^{\mathrm{3}} {x}}{\mathrm{3}}+{C} \\ $$
Answered by bobhans last updated on 06/Sep/20
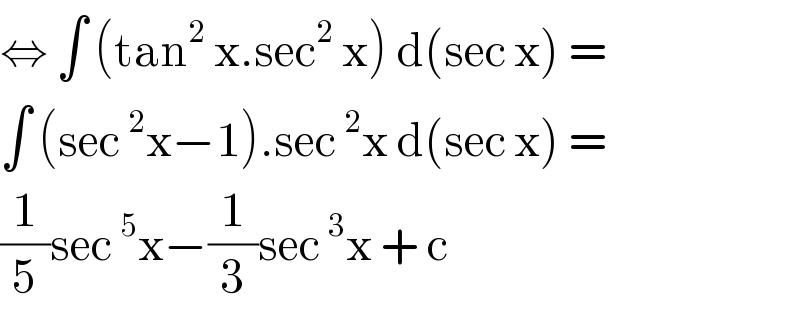
$$\Leftrightarrow\:\int\:\left(\mathrm{tan}^{\mathrm{2}} \:\mathrm{x}.\mathrm{sec}^{\mathrm{2}} \:\mathrm{x}\right)\:\mathrm{d}\left(\mathrm{sec}\:\mathrm{x}\right)\:=\: \\ $$$$\int\:\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right).\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{d}\left(\mathrm{sec}\:\mathrm{x}\right)\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sec}\:^{\mathrm{5}} \mathrm{x}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sec}\:^{\mathrm{3}} \mathrm{x}\:+\:\mathrm{c} \\ $$
