
Question Number 111342 by pete last updated on 03/Sep/20

$$\mathrm{When}\:\mathrm{the}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{a}\:\mathrm{Geometric}\:\mathrm{Progression}\left(\mathrm{GP}\right) \\ $$$$\mathrm{with}\:\mathrm{common}\:\mathrm{ratio}\:\mathrm{r}=\mathrm{2}\:\mathrm{is}\:\mathrm{added}\:\mathrm{to}\:\mathrm{the}\:\mathrm{corresponding}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{an}\:\mathrm{Arithmetic}\:\mathrm{Provression}\:\left(\mathrm{AP}\right), \\ $$$$\mathrm{a}\:\mathrm{new}\:\mathrm{sequence}\:\mathrm{is}\:\mathrm{formed}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{first}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{GP}\:\mathrm{and}\:\mathrm{AP}\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:\mathrm{and}\:\mathrm{the}\:\mathrm{first} \\ $$$$\mathrm{three}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{new}\:\mathrm{sequence}\:\mathrm{are} \\ $$$$\mathrm{3},\:\mathrm{7}\:\mathrm{and}\:\mathrm{11}\:\mathrm{respectively},\:\mathrm{find}\:\mathrm{the}\:\mathrm{n}^{\mathrm{th}} \:\mathrm{term} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{seauence}. \\ $$
Answered by Rasheed.Sindhi last updated on 03/Sep/20
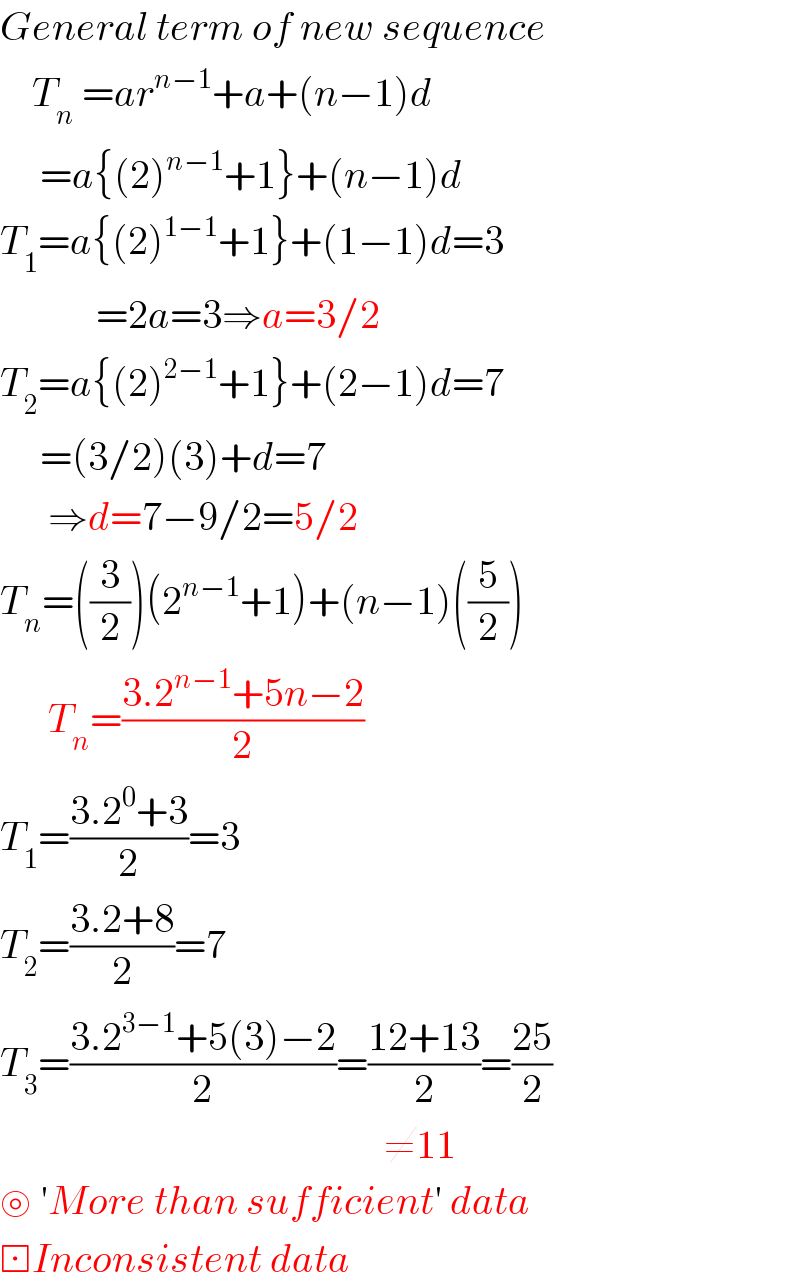
$${General}\:{term}\:{of}\:{new}\:{sequence} \\ $$$$\:\:\:\:{T}_{{n}} \:={ar}^{{n}−\mathrm{1}} +{a}+\left({n}−\mathrm{1}\right){d} \\ $$$$\:\:\:\:\:={a}\left\{\left(\mathrm{2}\right)^{{n}−\mathrm{1}} +\mathrm{1}\right\}+\left({n}−\mathrm{1}\right){d} \\ $$$${T}_{\mathrm{1}} ={a}\left\{\left(\mathrm{2}\right)^{\mathrm{1}−\mathrm{1}} +\mathrm{1}\right\}+\left(\mathrm{1}−\mathrm{1}\right){d}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{a}=\mathrm{3}\Rightarrow{a}=\mathrm{3}/\mathrm{2} \\ $$$${T}_{\mathrm{2}} ={a}\left\{\left(\mathrm{2}\right)^{\mathrm{2}−\mathrm{1}} +\mathrm{1}\right\}+\left(\mathrm{2}−\mathrm{1}\right){d}=\mathrm{7} \\ $$$$\:\:\:\:\:=\left(\mathrm{3}/\mathrm{2}\right)\left(\mathrm{3}\right)+{d}=\mathrm{7} \\ $$$$\:\:\:\:\:\:\Rightarrow{d}=\mathrm{7}−\mathrm{9}/\mathrm{2}=\mathrm{5}/\mathrm{2} \\ $$$${T}_{{n}} =\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{1}\right)+\left({n}−\mathrm{1}\right)\left(\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:{T}_{{n}} =\frac{\mathrm{3}.\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{5}{n}−\mathrm{2}}{\mathrm{2}} \\ $$$${T}_{\mathrm{1}} =\frac{\mathrm{3}.\mathrm{2}^{\mathrm{0}} +\mathrm{3}}{\mathrm{2}}=\mathrm{3} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{3}.\mathrm{2}+\mathrm{8}}{\mathrm{2}}=\mathrm{7} \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{3}.\mathrm{2}^{\mathrm{3}−\mathrm{1}} +\mathrm{5}\left(\mathrm{3}\right)−\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{12}+\mathrm{13}}{\mathrm{2}}=\frac{\mathrm{25}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\neq\mathrm{11} \\ $$$$\circledcirc\:'{More}\:{than}\:{sufficient}'\:{data} \\ $$$$\boxdot{Inconsistent}\:{data} \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
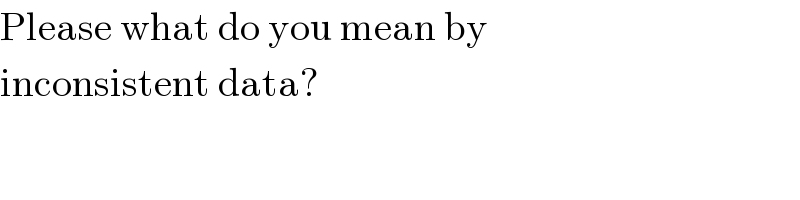
$$\mathrm{Please}\:\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{by} \\ $$$$\mathrm{inconsistent}\:\mathrm{data}? \\ $$
Commented by Rasheed.Sindhi last updated on 03/Sep/20

$${Contrdiction}\:{between}\:{data}.{Like} \\ $$$${here}\:{T}_{\mathrm{3}} =\mathrm{11}\:{is}\:{given}\:{but}\:{using} \\ $$$${other}\:{data}\:{we}\:{calculate}\:{T}_{\mathrm{3}} =\mathrm{25}/\mathrm{2} \\ $$$${T}_{\mathrm{3}} \:{same}\:{time}\:{can}'{t}\:{be}\:{equal}\:{to} \\ $$$${two}\:{values}! \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
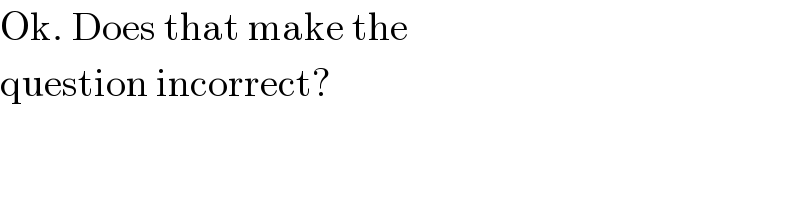
$$\mathrm{Ok}.\:\mathrm{Does}\:\mathrm{that}\:\mathrm{make}\:\mathrm{the} \\ $$$$\mathrm{question}\:\mathrm{incorrect}? \\ $$
Commented by Rasheed.Sindhi last updated on 03/Sep/20

$${Of}\:{course}! \\ $$
Commented by pete last updated on 03/Sep/20
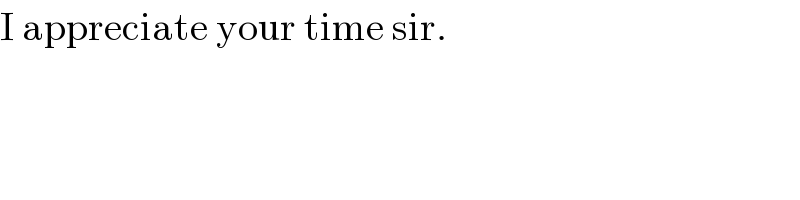
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
