
Question Number 111208 by Aziztisffola last updated on 02/Sep/20
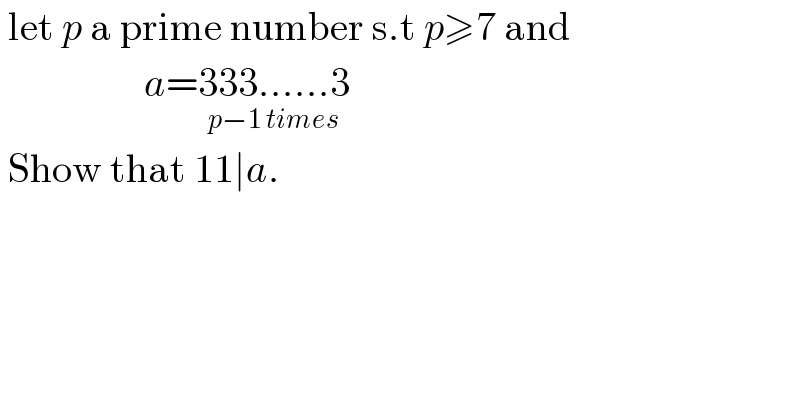
$$\:\mathrm{let}\:{p}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{number}\:\mathrm{s}.\mathrm{t}\:{p}\geqslant\mathrm{7}\:\mathrm{and}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=\underset{{p}−\mathrm{1}\:{times}} {\mathrm{333}......\mathrm{3}} \\ $$$$\:\mathrm{Show}\:\mathrm{that}\:\mathrm{11}\mid{a}. \\ $$
Commented by mr W last updated on 02/Sep/20
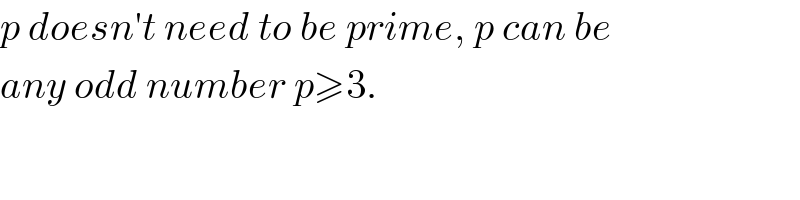
$${p}\:{doesn}'{t}\:{need}\:{to}\:{be}\:{prime},\:{p}\:{can}\:{be} \\ $$$${any}\:{odd}\:{number}\:{p}\geqslant\mathrm{3}. \\ $$
Commented by mr W last updated on 02/Sep/20
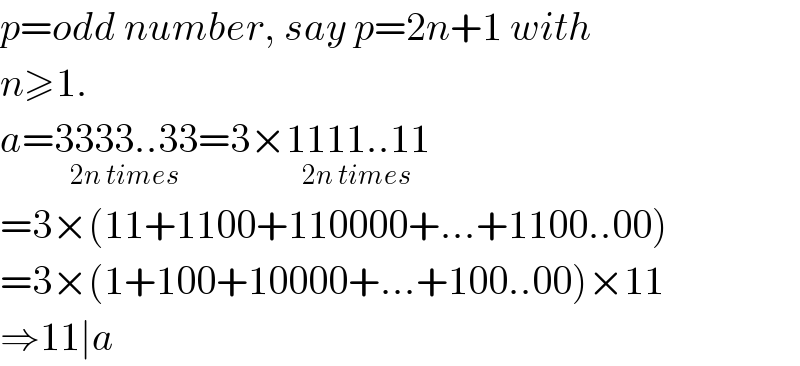
$${p}={odd}\:{number},\:{say}\:{p}=\mathrm{2}{n}+\mathrm{1}\:{with} \\ $$$${n}\geqslant\mathrm{1}. \\ $$$${a}=\underset{\mathrm{2}{n}\:{times}} {\mathrm{3333}..\mathrm{33}}=\mathrm{3}×\underset{\mathrm{2}{n}\:{times}} {\mathrm{1111}..\mathrm{11}} \\ $$$$=\mathrm{3}×\left(\mathrm{11}+\mathrm{1100}+\mathrm{110000}+...+\mathrm{1100}..\mathrm{00}\right) \\ $$$$=\mathrm{3}×\left(\mathrm{1}+\mathrm{100}+\mathrm{10000}+...+\mathrm{100}..\mathrm{00}\right)×\mathrm{11} \\ $$$$\Rightarrow\mathrm{11}\mid{a} \\ $$
Commented by Aziztisffola last updated on 02/Sep/20

$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{you}. \\ $$
Answered by Aziztisffola last updated on 02/Sep/20
![My answer a= 3+3×10+...+3×10^p =3(1+10+10^2 +...+10^p ) =3(((10^(p+1) −1)/9))=((10^(p+1) −1)/3) ⇒ 3a=10^(p+1) −1 10≡−1[11] ⇒10^(p+1) ≡1[11] (p+1 is even) ⇒ 10^(p+1) −1≡0[11] ⇒ 3a≡0[11] ⇒11∣3a ⇒^(3∧11=1) 11∣a](Q111221.png)
$$\mathrm{My}\:\mathrm{answer}\: \\ $$$$\:{a}=\:\mathrm{3}+\mathrm{3}×\mathrm{10}+...+\mathrm{3}×\mathrm{10}^{{p}} \\ $$$$\:\:\:=\mathrm{3}\left(\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} +...+\mathrm{10}^{{p}} \right) \\ $$$$\:\:\:=\mathrm{3}\left(\frac{\mathrm{10}^{{p}+\mathrm{1}} −\mathrm{1}}{\mathrm{9}}\right)=\frac{\mathrm{10}^{{p}+\mathrm{1}} −\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{3}{a}=\mathrm{10}^{{p}+\mathrm{1}} −\mathrm{1} \\ $$$$\:\mathrm{10}\equiv−\mathrm{1}\left[\mathrm{11}\right]\:\Rightarrow\mathrm{10}^{{p}+\mathrm{1}} \equiv\mathrm{1}\left[\mathrm{11}\right]\:\:\left({p}+\mathrm{1}\:{is}\:{even}\right) \\ $$$$\Rightarrow\:\mathrm{10}^{{p}+\mathrm{1}} −\mathrm{1}\equiv\mathrm{0}\left[\mathrm{11}\right] \\ $$$$\Rightarrow\:\mathrm{3}{a}\equiv\mathrm{0}\left[\mathrm{11}\right]\:\Rightarrow\mathrm{11}\mid\mathrm{3a}\:\:\overset{\mathrm{3}\wedge\mathrm{11}=\mathrm{1}} {\Rightarrow}\:\:\mathrm{11}\mid{a} \\ $$
