
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 110826 by Aina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{The}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{events}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{occurs}\:\mathrm{is}\:\mathrm{0}.\mathrm{7}\:\mathrm{and} \\ $$$$\mathrm{they}\:\mathrm{occur}\:\mathrm{simultaneously}\:\mathrm{with} \\ $$$$\mathrm{probability}\:\mathrm{0}.\mathrm{2}.\:\mathrm{Then}\:\mathrm{P}\left(\overset{−} {\mathrm{A}}\right)+\mathrm{P}\left(\bar {\mathrm{B}}\right)\:= \\ $$
Commented by kaivan.ahmadi last updated on 30/Aug/20
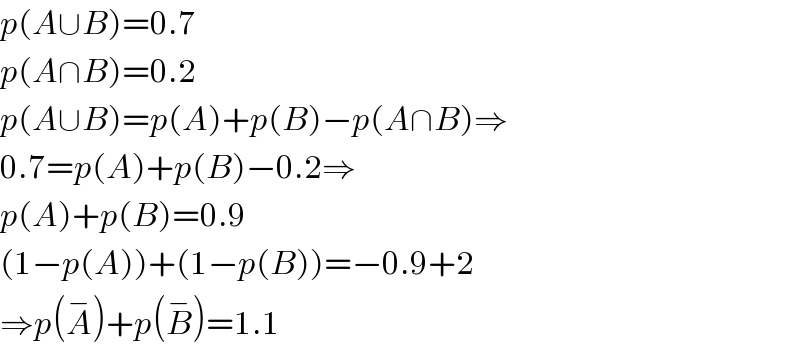
$${p}\left({A}\cup{B}\right)=\mathrm{0}.\mathrm{7} \\ $$$${p}\left({A}\cap{B}\right)=\mathrm{0}.\mathrm{2} \\ $$$${p}\left({A}\cup{B}\right)={p}\left({A}\right)+{p}\left({B}\right)−{p}\left({A}\cap{B}\right)\Rightarrow \\ $$$$\mathrm{0}.\mathrm{7}={p}\left({A}\right)+{p}\left({B}\right)−\mathrm{0}.\mathrm{2}\Rightarrow \\ $$$${p}\left({A}\right)+{p}\left({B}\right)=\mathrm{0}.\mathrm{9} \\ $$$$\left(\mathrm{1}−{p}\left({A}\right)\right)+\left(\mathrm{1}−{p}\left({B}\right)\right)=−\mathrm{0}.\mathrm{9}+\mathrm{2} \\ $$$$\Rightarrow{p}\left(\overset{−} {{A}}\right)+{p}\left(\overset{−} {{B}}\right)=\mathrm{1}.\mathrm{1} \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20
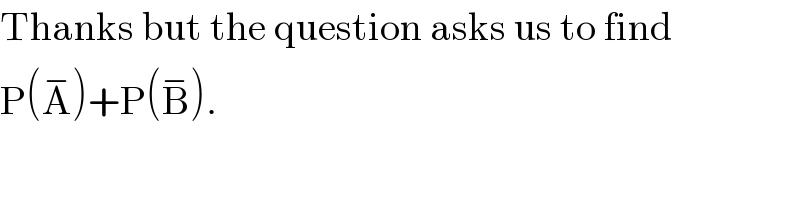
$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{the}\:\mathrm{question}\:\mathrm{asks}\:\mathrm{us}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{P}\left(\overset{−} {\mathrm{A}}\right)+\mathrm{P}\left(\overset{−} {\mathrm{B}}\right). \\ $$
Commented by Aina Samuel Temidayo last updated on 31/Aug/20

$$\mathrm{Yes}. \\ $$
Commented by Aina Samuel Temidayo last updated on 31/Aug/20
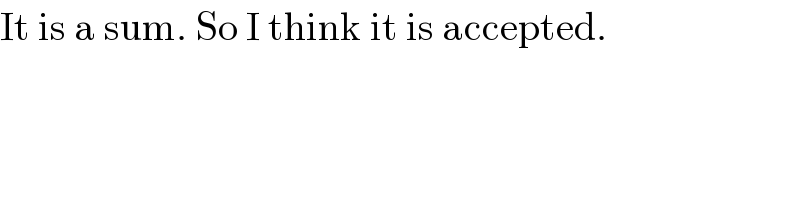
$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{sum}.\:\mathrm{So}\:\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\mathrm{accepted}. \\ $$
Commented by kaivan.ahmadi last updated on 31/Aug/20

$$\mathrm{0}\leqslant{p}\left(\overset{−} {{A}}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{0}\leqslant{p}\left(\overset{−} {{B}}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{0}\leqslant{p}\left(\overset{−} {{A}}\right)+{p}\left(\overset{−} {{B}}\right)\leqslant\mathrm{2} \\ $$
Commented by Her_Majesty last updated on 31/Aug/20

$${P}\left(\overset{−} {{A}}\right)+{P}\left(\overset{−} {{B}}\right)\neq{P}\left(\overset{−} {{A}}\wedge\overset{−} {{B}}\right) \\ $$$${the}\:{sum}\:{of}\:\mathrm{2}\:{independent}\:{probabilities}\:{is} \\ $$$${a}\:{senseless}\:{value}. \\ $$$${i}.{e}.\:{the}\:{probability}\:{of}\:{a}\:{thrown}\:{dice}\:{showing} \\ $$$${not}\:\mathrm{6}\:{is}\:\frac{\mathrm{5}}{\mathrm{6}},\:{the}\:{one}\:{of}\:{a}\:{thrown}\:{coin}\:{showing} \\ $$$${head}\:{is}\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{the}\:{sum}\:{is}\:\frac{\mathrm{4}}{\mathrm{3}}\approx\mathrm{133\%} \\ $$
