
Question Number 110781 by Aina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{Between}\:\mathrm{a}\:\mathrm{square},\mathrm{a}\:\mathrm{triangle}\:\mathrm{and}\:\mathrm{a} \\ $$$$\mathrm{circle}\:\mathrm{of}\:\mathrm{the}\:\mathrm{same}\:\mathrm{perimeter},\:\mathrm{which} \\ $$$$\mathrm{shape}\:\mathrm{has}\:\mathrm{the}\:\mathrm{least}\:\mathrm{area}? \\ $$
Commented by mr W last updated on 30/Aug/20
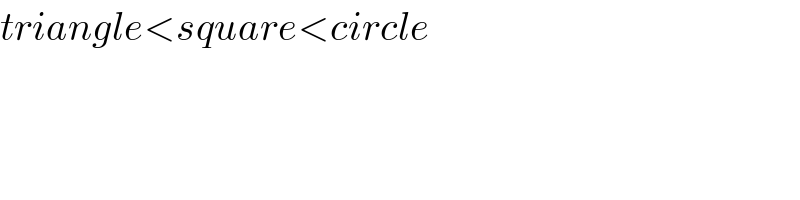
$${triangle}<{square}<{circle} \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{Solution}\:\mathrm{please}? \\ $$
Answered by $@y@m last updated on 30/Aug/20
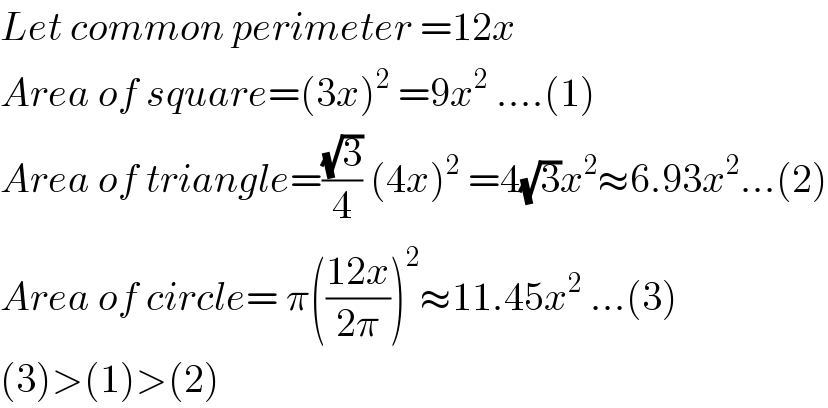
$${Let}\:{common}\:{perimeter}\:=\mathrm{12}{x} \\ $$$${Area}\:{of}\:{square}=\left(\mathrm{3}{x}\right)^{\mathrm{2}} \:=\mathrm{9}{x}^{\mathrm{2}} \:....\left(\mathrm{1}\right) \\ $$$${Area}\:{of}\:{triangle}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:\left(\mathrm{4}{x}\right)^{\mathrm{2}} \:=\mathrm{4}\sqrt{\mathrm{3}}{x}^{\mathrm{2}} \approx\mathrm{6}.\mathrm{93}{x}^{\mathrm{2}} ...\left(\mathrm{2}\right) \\ $$$${Area}\:{of}\:{circle}=\:\pi\left(\frac{\mathrm{12}{x}}{\mathrm{2}\pi}\right)^{\mathrm{2}} \approx\mathrm{11}.\mathrm{45}{x}^{\mathrm{2}} \:...\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{3}\right)>\left(\mathrm{1}\right)>\left(\mathrm{2}\right) \\ $$
Commented by Aina Samuel Temidayo last updated on 30/Aug/20

$$\mathrm{Thanks}. \\ $$
