
Question Number 110779 by ZiYangLee last updated on 30/Aug/20
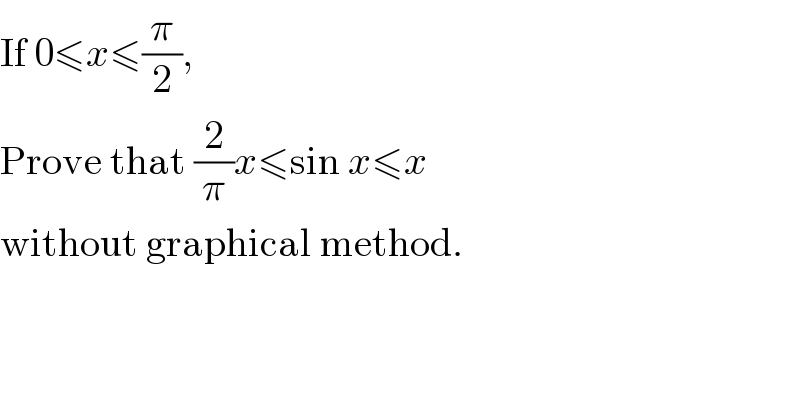
$$\mathrm{If}\:\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}, \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\frac{\mathrm{2}}{\pi}{x}\leqslant\mathrm{sin}\:{x}\leqslant{x} \\ $$$$\mathrm{without}\:\mathrm{graphical}\:\mathrm{method}. \\ $$
Answered by Her_Majesty last updated on 30/Aug/20
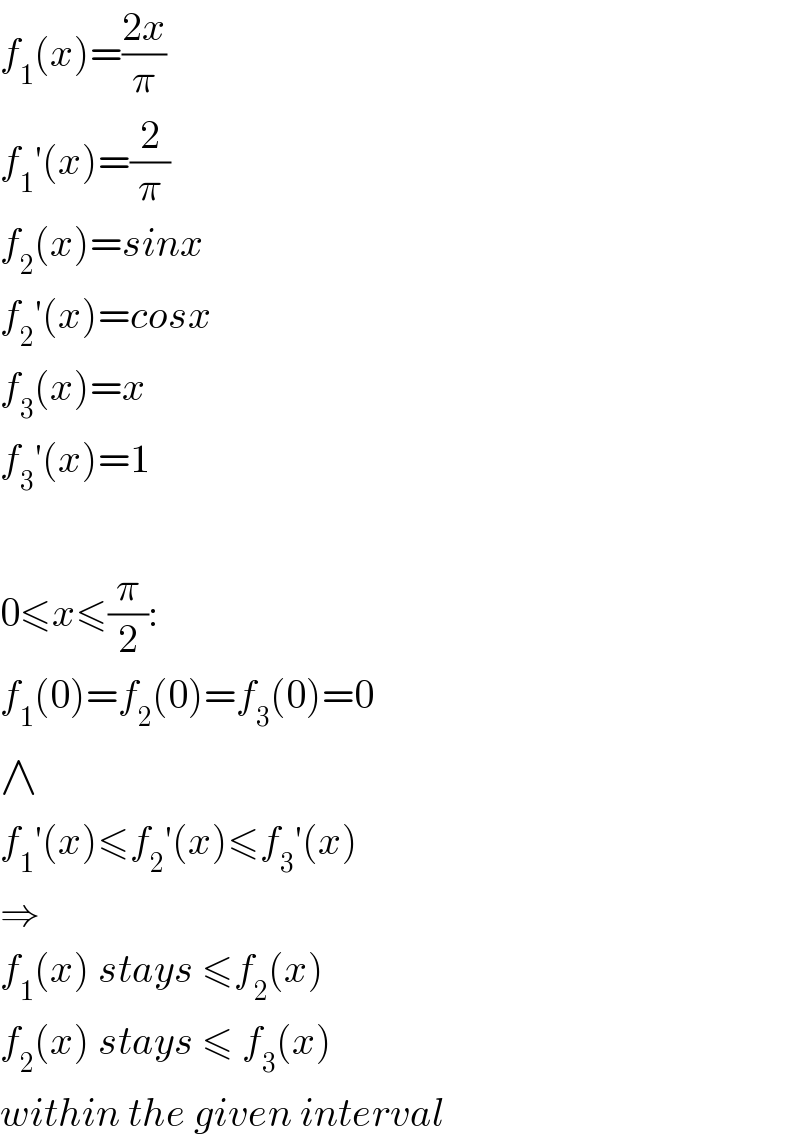
$${f}_{\mathrm{1}} \left({x}\right)=\frac{\mathrm{2}{x}}{\pi} \\ $$$${f}_{\mathrm{1}} '\left({x}\right)=\frac{\mathrm{2}}{\pi} \\ $$$${f}_{\mathrm{2}} \left({x}\right)={sinx} \\ $$$${f}_{\mathrm{2}} '\left({x}\right)={cosx} \\ $$$${f}_{\mathrm{3}} \left({x}\right)={x} \\ $$$${f}_{\mathrm{3}} '\left({x}\right)=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}}: \\ $$$${f}_{\mathrm{1}} \left(\mathrm{0}\right)={f}_{\mathrm{2}} \left(\mathrm{0}\right)={f}_{\mathrm{3}} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\wedge \\ $$$${f}_{\mathrm{1}} '\left({x}\right)\leqslant{f}_{\mathrm{2}} '\left({x}\right)\leqslant{f}_{\mathrm{3}} '\left({x}\right) \\ $$$$\Rightarrow \\ $$$${f}_{\mathrm{1}} \left({x}\right)\:{stays}\:\leqslant{f}_{\mathrm{2}} \left({x}\right) \\ $$$${f}_{\mathrm{2}} \left({x}\right)\:{stays}\:\leqslant\:{f}_{\mathrm{3}} \left({x}\right) \\ $$$${within}\:{the}\:{given}\:{interval} \\ $$
Commented by ZiYangLee last updated on 31/Aug/20

$$\mathrm{Thanks}! \\ $$
