Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 110136 by qwerty111 last updated on 27/Aug/20

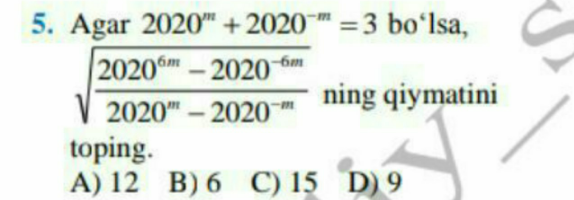
Answered by $@y@m last updated on 27/Aug/20

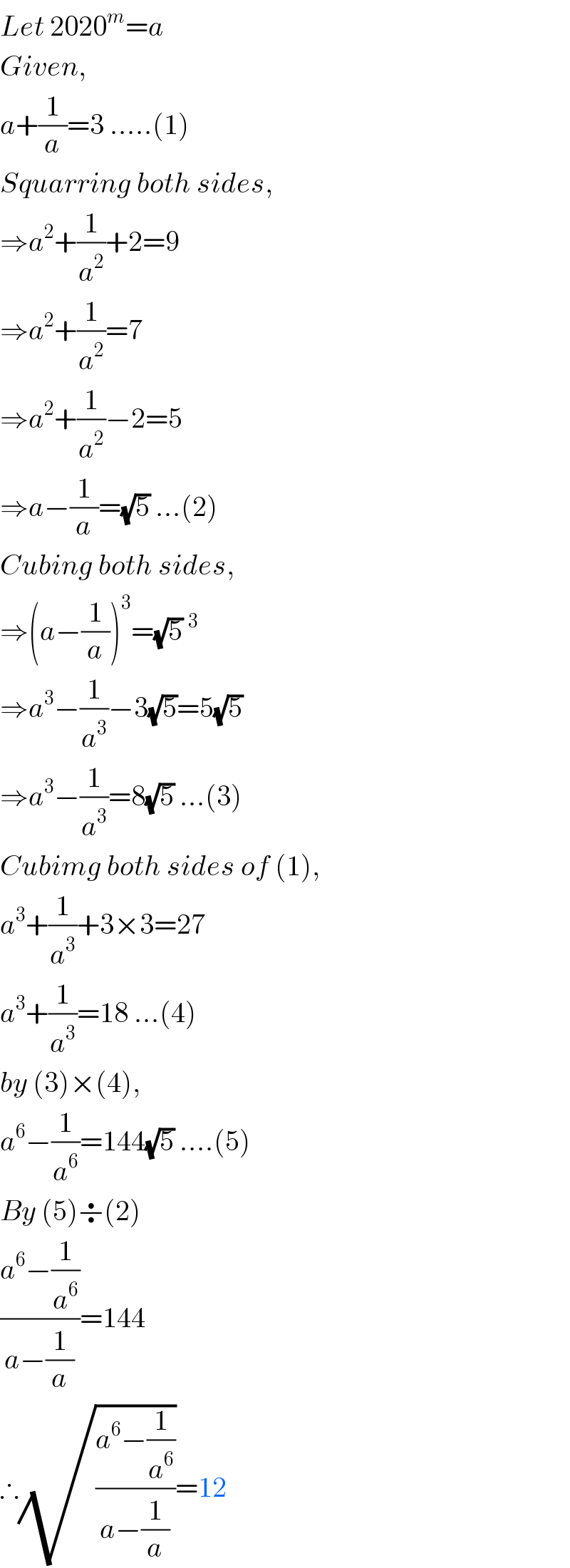
Let 2020^m =a Given, a+(1/a)=3 .....(1) Squarring both sides, ⇒a^2 +(1/a^2 )+2=9 ⇒a^2 +(1/a^2 )=7 ⇒a^2 +(1/a^2 )−2=5 ⇒a−(1/a)=(√5) ...(2) Cubing both sides, ⇒(a−(1/a))^3 =(√5)^3 ⇒a^3 −(1/a^3 )−3(√5)=5(√5) ⇒a^3 −(1/a^3 )=8(√5) ...(3) Cubimg both sides of (1), a^3 +(1/a^3 )+3×3=27 a^3 +(1/a^3 )=18 ...(4) by (3)×(4), a^6 −(1/a^6 )=144(√5) ....(5) By (5)÷(2) ((a^6 −(1/a^6 ))/(a−(1/a)))=144 ∴(√((a^6 −(1/a^6 ))/(a−(1/a))))=12

$${Let}\:\mathrm{2020}^{{m}} ={a}\: \\ $$$${Given}, \\ $$$${a}+\frac{\mathrm{1}}{{a}}=\mathrm{3}\:.....\left(\mathrm{1}\right) \\ $$$${Squarring}\:{both}\:{sides}, \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{2}=\mathrm{9} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }=\mathrm{7} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\mathrm{2}=\mathrm{5} \\ $$$$\Rightarrow{a}−\frac{\mathrm{1}}{{a}}=\sqrt{\mathrm{5}}\:...\left(\mathrm{2}\right) \\ $$$${Cubing}\:{both}\:{sides}, \\ $$$$\Rightarrow\left({a}−\frac{\mathrm{1}}{{a}}\right)^{\mathrm{3}} =\sqrt{\mathrm{5}}\:^{\mathrm{3}} \\ $$$$\Rightarrow{a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }−\mathrm{3}\sqrt{\mathrm{5}}=\mathrm{5}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{a}^{\mathrm{3}} −\frac{\mathrm{1}}{{a}^{\mathrm{3}} }=\mathrm{8}\sqrt{\mathrm{5}}\:...\left(\mathrm{3}\right) \\ $$$${Cubimg}\:{both}\:{sides}\:{of}\:\left(\mathrm{1}\right), \\ $$$${a}^{\mathrm{3}} +\frac{\mathrm{1}}{{a}^{\mathrm{3}} }+\mathrm{3}×\mathrm{3}=\mathrm{27} \\ $$$${a}^{\mathrm{3}} +\frac{\mathrm{1}}{{a}^{\mathrm{3}} }=\mathrm{18}\:...\left(\mathrm{4}\right) \\ $$$${by}\:\left(\mathrm{3}\right)×\left(\mathrm{4}\right), \\ $$$${a}^{\mathrm{6}} −\frac{\mathrm{1}}{{a}^{\mathrm{6}} }=\mathrm{144}\sqrt{\mathrm{5}}\:....\left(\mathrm{5}\right) \\ $$$${By}\:\left(\mathrm{5}\right)\boldsymbol{\div}\left(\mathrm{2}\right) \\ $$$$\frac{{a}^{\mathrm{6}} −\frac{\mathrm{1}}{{a}^{\mathrm{6}} }}{{a}−\frac{\mathrm{1}}{{a}}}=\mathrm{144} \\ $$$$\therefore\sqrt{\frac{{a}^{\mathrm{6}} −\frac{\mathrm{1}}{{a}^{\mathrm{6}} }}{{a}−\frac{\mathrm{1}}{{a}}}}=\mathrm{12} \\ $$

Answered by Sarah85 last updated on 27/Aug/20

x^m +x^(−m) =3 x^(2m) +1=3x^m x^(2m) −3x^m +1=0 x^m =((3±(√5))/2) ⇒ x^(6m) =(((3±(√5))/2))^6 =161±72(√5) x^(6m) −x^(−6m) =±144(√5) x^m −x^(−m) =±(√5) ⇒ answer is 12 independent of x

$${x}^{{m}} +{x}^{−{m}} =\mathrm{3} \\ $$$${x}^{\mathrm{2}{m}} +\mathrm{1}=\mathrm{3}{x}^{{m}} \\ $$$${x}^{\mathrm{2}{m}} −\mathrm{3}{x}^{{m}} +\mathrm{1}=\mathrm{0} \\ $$$${x}^{{m}} =\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}^{\mathrm{6}{m}} =\left(\frac{\mathrm{3}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{6}} =\mathrm{161}\pm\mathrm{72}\sqrt{\mathrm{5}} \\ $$$${x}^{\mathrm{6}{m}} −{x}^{−\mathrm{6}{m}} =\pm\mathrm{144}\sqrt{\mathrm{5}} \\ $$$${x}^{{m}} −{x}^{−{m}} =\pm\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{12}\:\mathrm{independent}\:\mathrm{of}\:{x} \\ $$

Answered by Rasheed.Sindhi last updated on 27/Aug/20

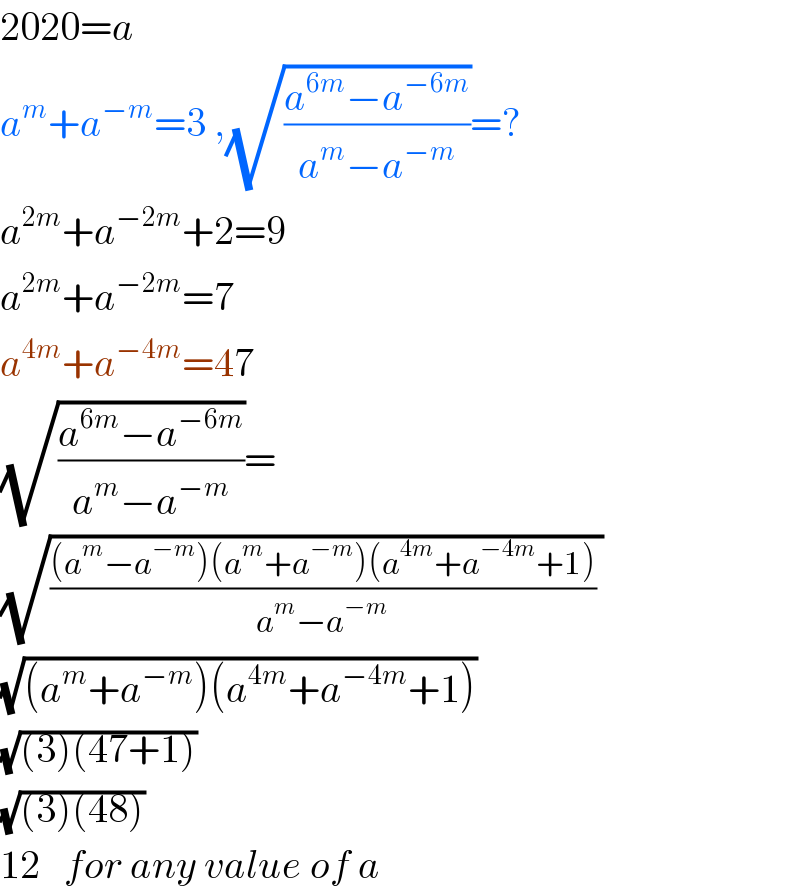
2020=a a^m +a^(−m) =3 ,(√((a^(6m) −a^(−6m) )/(a^m −a^(−m) )))=? a^(2m) +a^(−2m) +2=9 a^(2m) +a^(−2m) =7 a^(4m) +a^(−4m) =47 (√((a^(6m) −a^(−6m) )/(a^m −a^(−m) )))= (√((((a^m −a^(−m) )(a^m +a^(−m) )(a^(4m) +a^(−4m) +1))/(a^m −a^(−m) )) )) (√((a^m +a^(−m) )(a^(4m) +a^(−4m) +1))) (√((3)(47+1))) (√((3)(48))) 12 for any value of a

$$\mathrm{2020}={a} \\ $$$${a}^{{m}} +{a}^{−{m}} =\mathrm{3}\:,\sqrt{\frac{{a}^{\mathrm{6}{m}} −{a}^{−\mathrm{6}{m}} }{{a}^{{m}} −{a}^{−{m}} }}=? \\ $$$${a}^{\mathrm{2}{m}} +{a}^{−\mathrm{2}{m}} +\mathrm{2}=\mathrm{9} \\ $$$${a}^{\mathrm{2}{m}} +{a}^{−\mathrm{2}{m}} =\mathrm{7} \\ $$$${a}^{\mathrm{4}{m}} +{a}^{−\mathrm{4}{m}} =\mathrm{47} \\ $$$$\sqrt{\frac{{a}^{\mathrm{6}{m}} −{a}^{−\mathrm{6}{m}} }{{a}^{{m}} −{a}^{−{m}} }}= \\ $$$$\sqrt{\frac{\left({a}^{{m}} −{a}^{−{m}} \right)\left({a}^{{m}} +{a}^{−{m}} \right)\left({a}^{\mathrm{4}{m}} +{a}^{−\mathrm{4}{m}} +\mathrm{1}\right)}{{a}^{{m}} −{a}^{−{m}} }\:} \\ $$$$\sqrt{\left({a}^{{m}} +{a}^{−{m}} \right)\left({a}^{\mathrm{4}{m}} +{a}^{−\mathrm{4}{m}} +\mathrm{1}\right)} \\ $$$$\sqrt{\left(\mathrm{3}\right)\left(\mathrm{47}+\mathrm{1}\right)} \\ $$$$\sqrt{\left(\mathrm{3}\right)\left(\mathrm{48}\right)} \\ $$$$\mathrm{12}\:\:\:{for}\:{any}\:{value}\:{of}\:{a} \\ $$

Answered by Rasheed.Sindhi last updated on 27/Aug/20

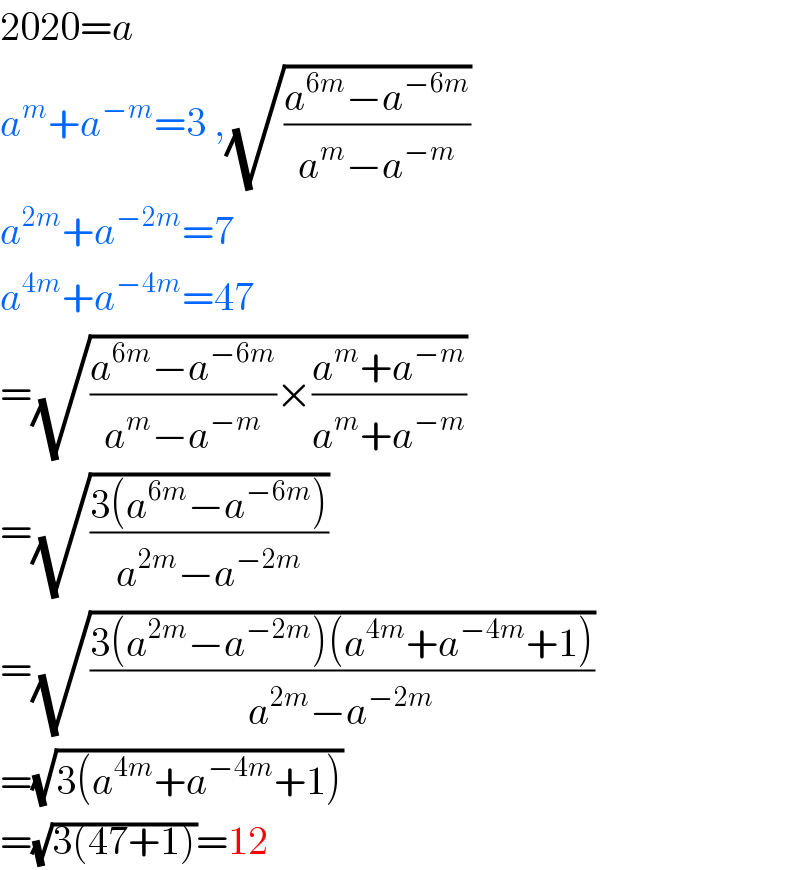
2020=a a^m +a^(−m) =3 ,(√((a^(6m) −a^(−6m) )/(a^m −a^(−m) ))) a^(2m) +a^(−2m) =7 a^(4m) +a^(−4m) =47 =(√(((a^(6m) −a^(−6m) )/(a^m −a^(−m) ))×((a^m +a^(−m) )/(a^m +a^(−m) )))) =(√((3(a^(6m) −a^(−6m) ))/(a^(2m) −a^(−2m) ))) =(√((3(a^(2m) −a^(−2m) )(a^(4m) +a^(−4m) +1))/(a^(2m) −a^(−2m) ))) =(√(3(a^(4m) +a^(−4m) +1))) =(√(3(47+1)))=12

$$\mathrm{2020}={a} \\ $$$${a}^{{m}} +{a}^{−{m}} =\mathrm{3}\:,\sqrt{\frac{{a}^{\mathrm{6}{m}} −{a}^{−\mathrm{6}{m}} }{{a}^{{m}} −{a}^{−{m}} }} \\ $$$${a}^{\mathrm{2}{m}} +{a}^{−\mathrm{2}{m}} =\mathrm{7} \\ $$$${a}^{\mathrm{4}{m}} +{a}^{−\mathrm{4}{m}} =\mathrm{47} \\ $$$$=\sqrt{\frac{{a}^{\mathrm{6}{m}} −{a}^{−\mathrm{6}{m}} }{{a}^{{m}} −{a}^{−{m}} }×\frac{{a}^{{m}} +{a}^{−{m}} }{{a}^{{m}} +{a}^{−{m}} }} \\ $$$$=\sqrt{\frac{\mathrm{3}\left({a}^{\mathrm{6}{m}} −{a}^{−\mathrm{6}{m}} \right)}{{a}^{\mathrm{2}{m}} −{a}^{−\mathrm{2}{m}} }} \\ $$$$=\sqrt{\frac{\mathrm{3}\left({a}^{\mathrm{2}{m}} −{a}^{−\mathrm{2}{m}} \right)\left({a}^{\mathrm{4}{m}} +{a}^{−\mathrm{4}{m}} +\mathrm{1}\right)}{{a}^{\mathrm{2}{m}} −{a}^{−\mathrm{2}{m}} }} \\ $$$$=\sqrt{\mathrm{3}\left({a}^{\mathrm{4}{m}} +{a}^{−\mathrm{4}{m}} +\mathrm{1}\right)} \\ $$$$=\sqrt{\mathrm{3}\left(\mathrm{47}+\mathrm{1}\right)}=\mathrm{12} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com