
Question Number 109923 by mathdave last updated on 26/Aug/20

$${find}\: \\ $$$${sin}\mathrm{3}\:\:\: \\ $$$${in}\:{surd}\:{form} \\ $$
Answered by malwan last updated on 26/Aug/20
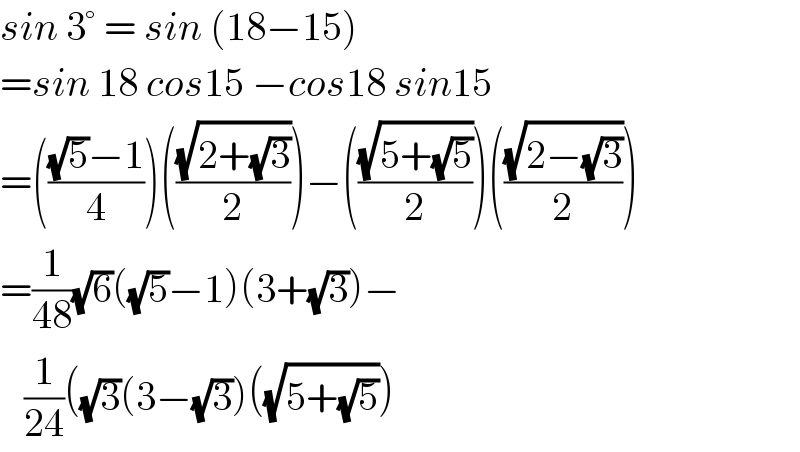
$${sin}\:\mathrm{3}°\:=\:{sin}\:\left(\mathrm{18}−\mathrm{15}\right) \\ $$$$={sin}\:\mathrm{18}\:{cos}\mathrm{15}\:−{cos}\mathrm{18}\:{sin}\mathrm{15} \\ $$$$=\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)\left(\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}}\right)−\left(\frac{\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}}{\mathrm{2}}\right)\left(\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{48}}\sqrt{\mathrm{6}}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\mathrm{3}+\sqrt{\mathrm{3}}\right)− \\ $$$$\:\:\:\frac{\mathrm{1}}{\mathrm{24}}\left(\sqrt{\mathrm{3}}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}\right)\right. \\ $$
Commented by mathdave last updated on 26/Aug/20

$${correct}\: \\ $$
Commented by malwan last updated on 26/Aug/20

$${thank}\:{you}\:{sir} \\ $$
