
Question Number 108870 by 150505R last updated on 19/Aug/20
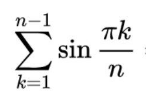
Commented by Dwaipayan Shikari last updated on 19/Aug/20

$${cot}\frac{\pi}{\mathrm{2}{n}} \\ $$
Answered by Ar Brandon last updated on 19/Aug/20
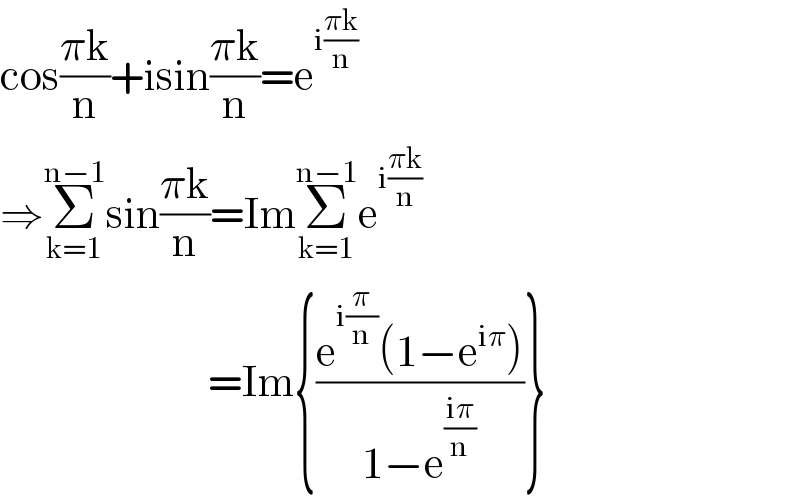
$$\mathrm{cos}\frac{\pi\mathrm{k}}{\mathrm{n}}+\mathrm{isin}\frac{\pi\mathrm{k}}{\mathrm{n}}=\mathrm{e}^{\mathrm{i}\frac{\pi\mathrm{k}}{\mathrm{n}}} \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{sin}\frac{\pi\mathrm{k}}{\mathrm{n}}=\mathrm{Im}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{e}^{\mathrm{i}\frac{\pi\mathrm{k}}{\mathrm{n}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{Im}\left\{\frac{\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{n}}} \left(\mathrm{1}−\mathrm{e}^{\mathrm{i}\pi} \right)}{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{n}}} }\right\} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Aug/20
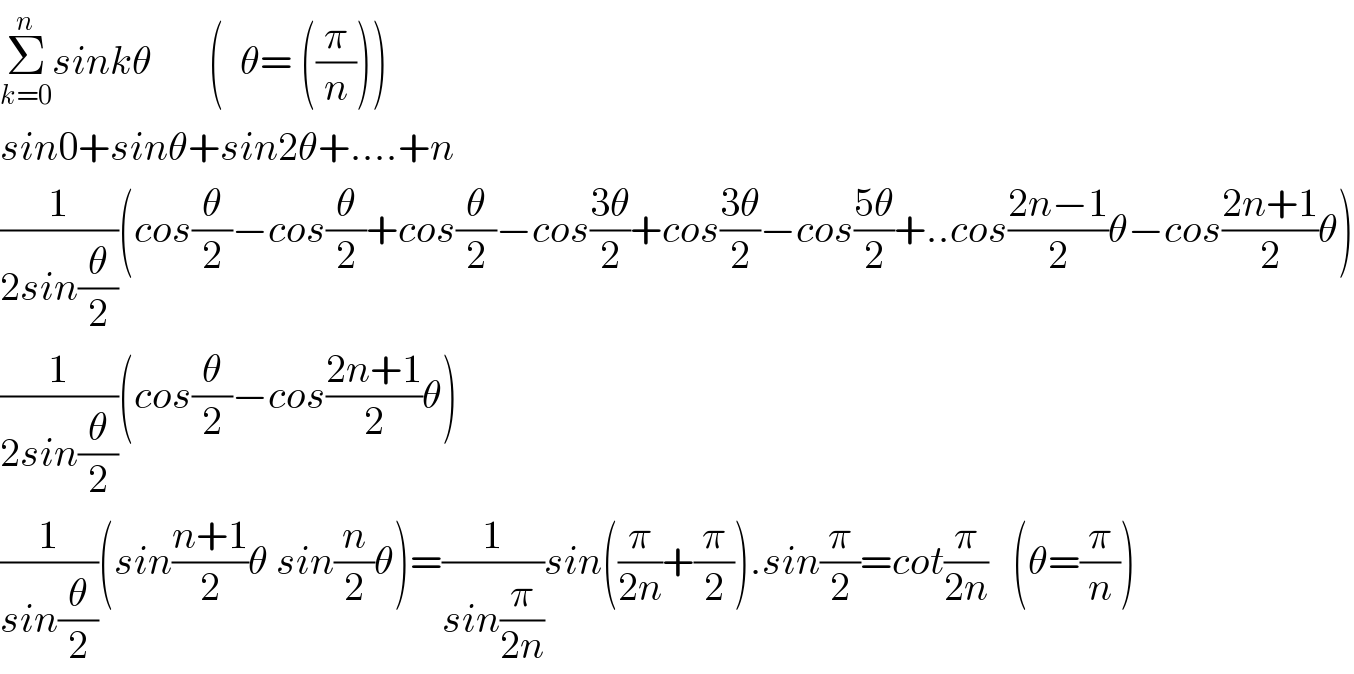
$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{sink}\theta\:\:\:\:\:\:\:\left(\:\:\theta=\:\left(\frac{\pi}{{n}}\right)\right) \\ $$$${sin}\mathrm{0}+{sin}\theta+{sin}\mathrm{2}\theta+....+{n} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({cos}\frac{\theta}{\mathrm{2}}−{cos}\frac{\theta}{\mathrm{2}}+{cos}\frac{\theta}{\mathrm{2}}−{cos}\frac{\mathrm{3}\theta}{\mathrm{2}}+{cos}\frac{\mathrm{3}\theta}{\mathrm{2}}−{cos}\frac{\mathrm{5}\theta}{\mathrm{2}}+..{cos}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\theta−{cos}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({cos}\frac{\theta}{\mathrm{2}}−{cos}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$$$\frac{\mathrm{1}}{{sin}\frac{\theta}{\mathrm{2}}}\left({sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\:{sin}\frac{{n}}{\mathrm{2}}\theta\right)=\frac{\mathrm{1}}{{sin}\frac{\pi}{\mathrm{2}{n}}}{sin}\left(\frac{\pi}{\mathrm{2}{n}}+\frac{\pi}{\mathrm{2}}\right).{sin}\frac{\pi}{\mathrm{2}}={cot}\frac{\pi}{\mathrm{2}{n}}\:\:\:\left(\theta=\frac{\pi}{{n}}\right) \\ $$
