
Question Number 10864 by chux last updated on 28/Feb/17

Answered by ridwan balatif last updated on 28/Feb/17
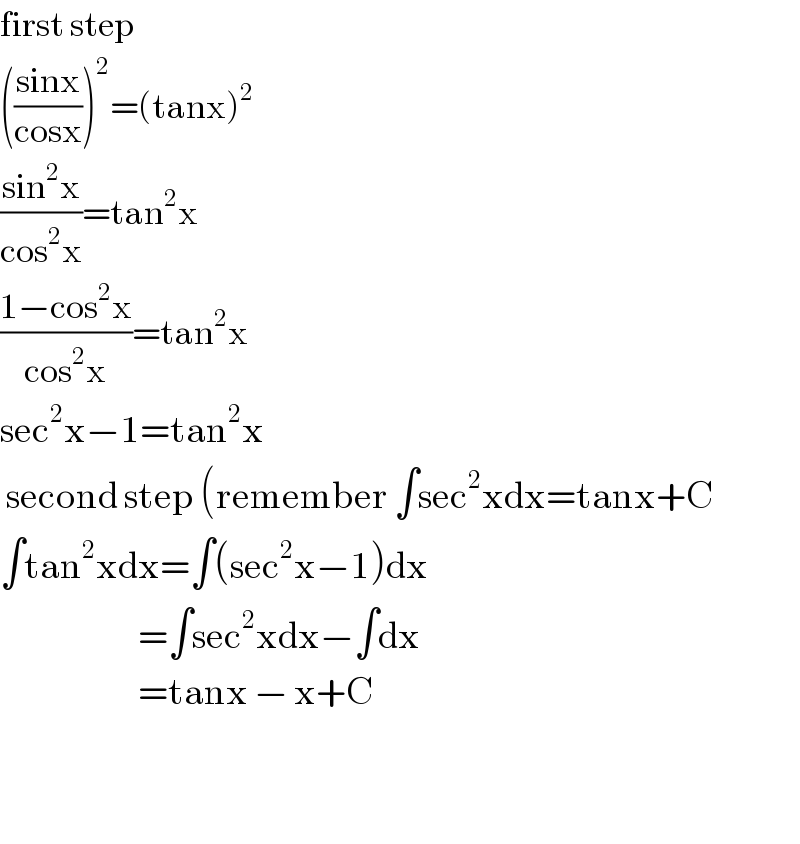
$$\mathrm{first}\:\mathrm{step} \\ $$$$\left(\frac{\mathrm{sinx}}{\mathrm{cosx}}\right)^{\mathrm{2}} =\left(\mathrm{tanx}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}=\mathrm{tan}^{\mathrm{2}} \mathrm{x} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}=\mathrm{tan}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}=\mathrm{tan}^{\mathrm{2}} \mathrm{x} \\ $$$$\:\mathrm{second}\:\mathrm{step}\:\left(\mathrm{remember}\:\int\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}=\mathrm{tanx}+\mathrm{C}\right. \\ $$$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{xdx}=\int\left(\mathrm{sec}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int\mathrm{sec}^{\mathrm{2}} \mathrm{xdx}−\int\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{tanx}\:−\:\mathrm{x}+\mathrm{C} \\ $$$$ \\ $$$$ \\ $$
Commented by chux last updated on 28/Feb/17
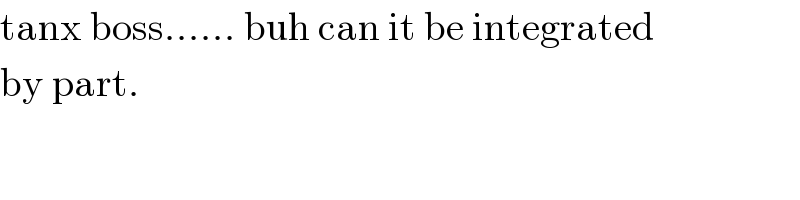
$$\mathrm{tanx}\:\mathrm{boss}......\:\mathrm{buh}\:\mathrm{can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{integrated} \\ $$$$\mathrm{by}\:\mathrm{part}. \\ $$
