
Question Number 108000 by ZiYangLee last updated on 13/Aug/20
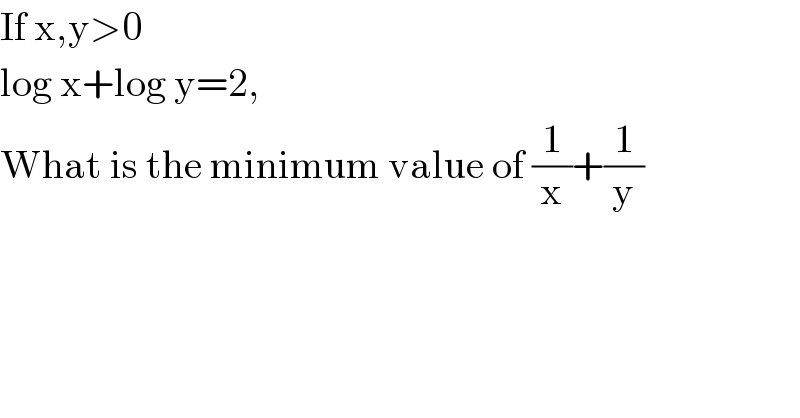
$$\mathrm{If}\:\mathrm{x},\mathrm{y}>\mathrm{0}\: \\ $$ $$\mathrm{log}\:\mathrm{x}+\mathrm{log}\:\mathrm{y}=\mathrm{2}, \\ $$ $$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}} \\ $$
Answered by mr W last updated on 13/Aug/20
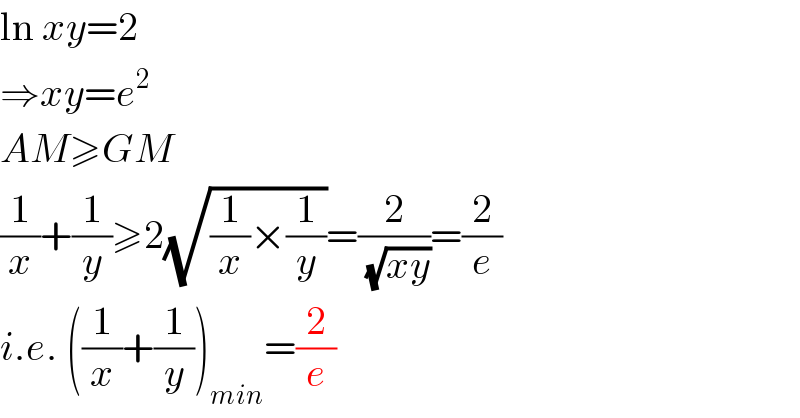
$$\mathrm{ln}\:{xy}=\mathrm{2} \\ $$ $$\Rightarrow{xy}={e}^{\mathrm{2}} \\ $$ $${AM}\geqslant{GM} \\ $$ $$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\geqslant\mathrm{2}\sqrt{\frac{\mathrm{1}}{{x}}×\frac{\mathrm{1}}{{y}}}=\frac{\mathrm{2}}{\:\sqrt{{xy}}}=\frac{\mathrm{2}}{{e}} \\ $$ $${i}.{e}.\:\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}\right)_{{min}} =\frac{\mathrm{2}}{{e}} \\ $$
