
Question Number 107993 by mohammad17 last updated on 13/Aug/20
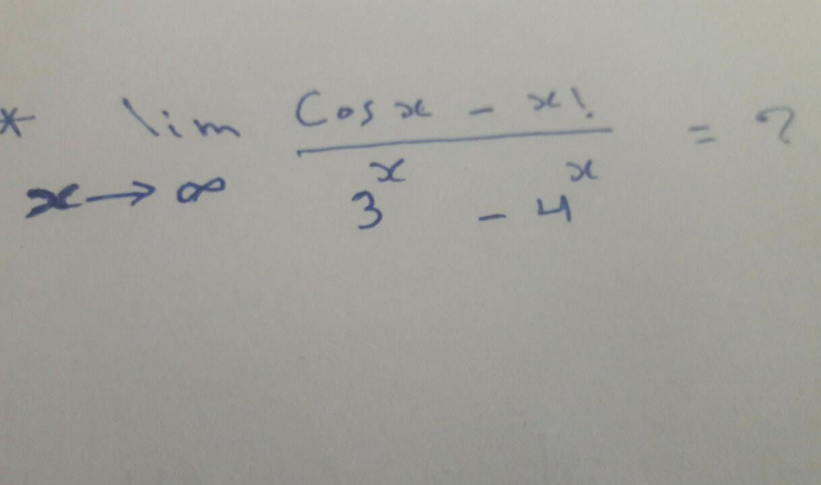
Answered by hgrocks last updated on 13/Aug/20

$$\infty \\ $$
Commented by mohammad17 last updated on 13/Aug/20
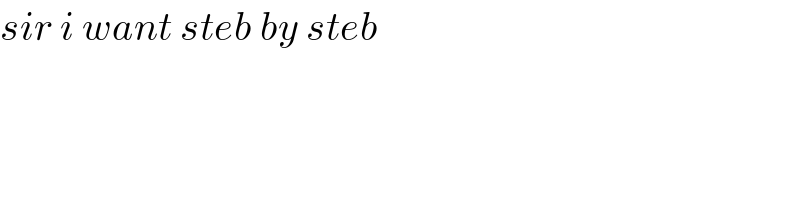
$${sir}\:{i}\:{want}\:{steb}\:{by}\:{steb}\: \\ $$
Answered by hgrocks last updated on 13/Aug/20
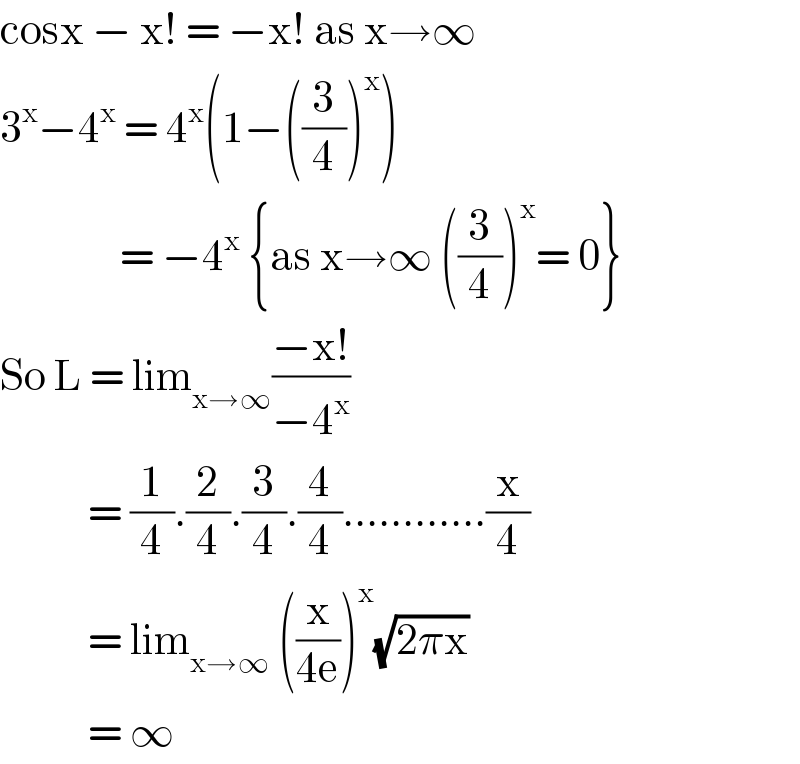
$$\mathrm{cosx}\:−\:\mathrm{x}!\:=\:−\mathrm{x}!\:\mathrm{as}\:\mathrm{x}\rightarrow\infty \\ $$$$\mathrm{3}^{\mathrm{x}} −\mathrm{4}^{\mathrm{x}} \:=\:\mathrm{4}^{\mathrm{x}} \left(\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{x}} \right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{4}^{\mathrm{x}} \:\left\{\mathrm{as}\:\mathrm{x}\rightarrow\infty\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{x}} =\:\mathrm{0}\right\} \\ $$$$\mathrm{So}\:\mathrm{L}\:=\:\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \frac{−\mathrm{x}!}{−\mathrm{4}^{\mathrm{x}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{2}}{\mathrm{4}}.\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{4}}{\mathrm{4}}............\frac{\mathrm{x}}{\mathrm{4}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \:\left(\frac{\mathrm{x}}{\mathrm{4e}}\right)^{\mathrm{x}} \sqrt{\mathrm{2}\pi\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\infty \\ $$
Commented by mohammad17 last updated on 13/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 13/Aug/20
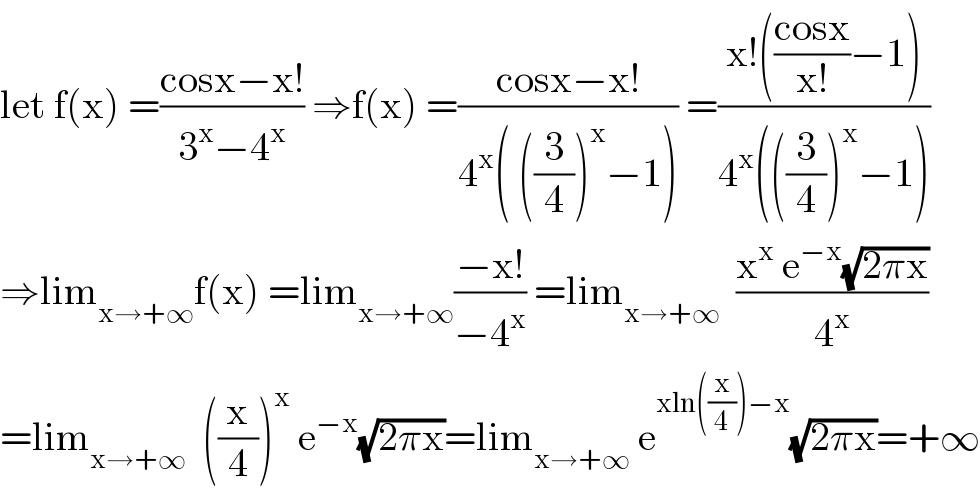
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{cosx}−\mathrm{x}!}{\mathrm{3}^{\mathrm{x}} −\mathrm{4}^{\mathrm{x}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{cosx}−\mathrm{x}!}{\mathrm{4}^{\mathrm{x}} \left(\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{x}} −\mathrm{1}\right)}\:=\frac{\mathrm{x}!\left(\frac{\mathrm{cosx}}{\mathrm{x}!}−\mathrm{1}\right)}{\mathrm{4}^{\mathrm{x}} \left(\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{x}} −\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \frac{−\mathrm{x}!}{−\mathrm{4}^{\mathrm{x}} }\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\frac{\mathrm{x}^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{x}} \sqrt{\mathrm{2}\pi\mathrm{x}}}{\mathrm{4}^{\mathrm{x}} } \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\left(\frac{\mathrm{x}}{\mathrm{4}}\right)^{\mathrm{x}} \:\mathrm{e}^{−\mathrm{x}} \sqrt{\mathrm{2}\pi\mathrm{x}}=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{e}^{\mathrm{xln}\left(\frac{\mathrm{x}}{\mathrm{4}}\right)−\mathrm{x}} \sqrt{\mathrm{2}\pi\mathrm{x}}=+\infty \\ $$
Commented by mohammad17 last updated on 13/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 13/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
