
Question Number 10675 by niraj last updated on 22/Feb/17
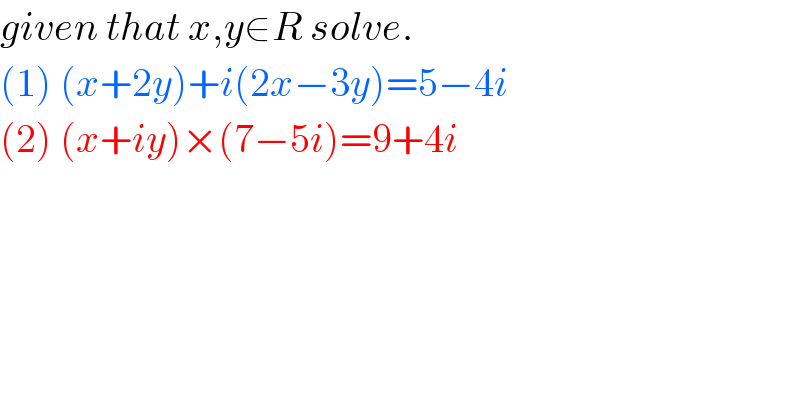
$${given}\:{that}\:{x},{y}\in{R}\:{solve}. \\ $$$$\left(\mathrm{1}\right)\:\left({x}+\mathrm{2}{y}\right)+{i}\left(\mathrm{2}{x}−\mathrm{3}{y}\right)=\mathrm{5}−\mathrm{4}{i} \\ $$$$\left(\mathrm{2}\right)\:\left({x}+{iy}\right)×\left(\mathrm{7}−\mathrm{5}{i}\right)=\mathrm{9}+\mathrm{4}{i} \\ $$
Commented by niraj last updated on 22/Feb/17
$${sir}\:{answer}\:{please} \\ $$
Answered by sandy_suhendra last updated on 22/Feb/17
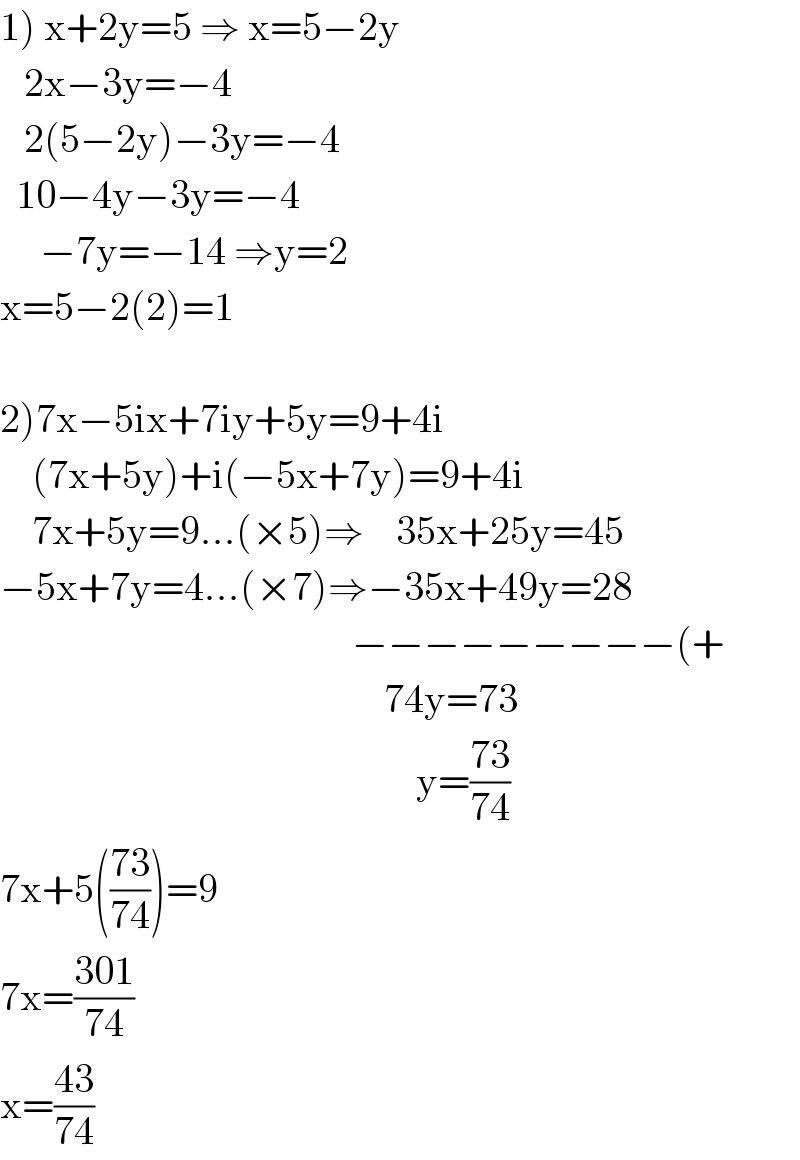
$$\left.\mathrm{1}\right)\:\mathrm{x}+\mathrm{2y}=\mathrm{5}\:\Rightarrow\:\mathrm{x}=\mathrm{5}−\mathrm{2y} \\ $$$$\:\:\:\mathrm{2x}−\mathrm{3y}=−\mathrm{4} \\ $$$$\:\:\:\mathrm{2}\left(\mathrm{5}−\mathrm{2y}\right)−\mathrm{3y}=−\mathrm{4} \\ $$$$\:\:\mathrm{10}−\mathrm{4y}−\mathrm{3y}=−\mathrm{4} \\ $$$$\:\:\:\:\:−\mathrm{7y}=−\mathrm{14}\:\Rightarrow\mathrm{y}=\mathrm{2} \\ $$$$\mathrm{x}=\mathrm{5}−\mathrm{2}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\mathrm{7x}−\mathrm{5ix}+\mathrm{7iy}+\mathrm{5y}=\mathrm{9}+\mathrm{4i} \\ $$$$\:\:\:\:\left(\mathrm{7x}+\mathrm{5y}\right)+\mathrm{i}\left(−\mathrm{5x}+\mathrm{7y}\right)=\mathrm{9}+\mathrm{4i} \\ $$$$\:\:\:\:\mathrm{7x}+\mathrm{5y}=\mathrm{9}...\left(×\mathrm{5}\right)\Rightarrow\:\:\:\:\mathrm{35x}+\mathrm{25y}=\mathrm{45} \\ $$$$−\mathrm{5x}+\mathrm{7y}=\mathrm{4}...\left(×\mathrm{7}\right)\Rightarrow−\mathrm{35x}+\mathrm{49y}=\mathrm{28}\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−−−\left(+\:\:\:\:\:\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{74y}=\mathrm{73} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}=\frac{\mathrm{73}}{\mathrm{74}} \\ $$$$\mathrm{7x}+\mathrm{5}\left(\frac{\mathrm{73}}{\mathrm{74}}\right)=\mathrm{9} \\ $$$$\mathrm{7x}=\frac{\mathrm{301}}{\mathrm{74}} \\ $$$$\mathrm{x}=\frac{\mathrm{43}}{\mathrm{74}} \\ $$
Commented by niraj last updated on 23/Feb/17
$${very}\:{very}\:{thanks}\:{sir} \\ $$
