
Question Number 10665 by FilupS last updated on 22/Feb/17
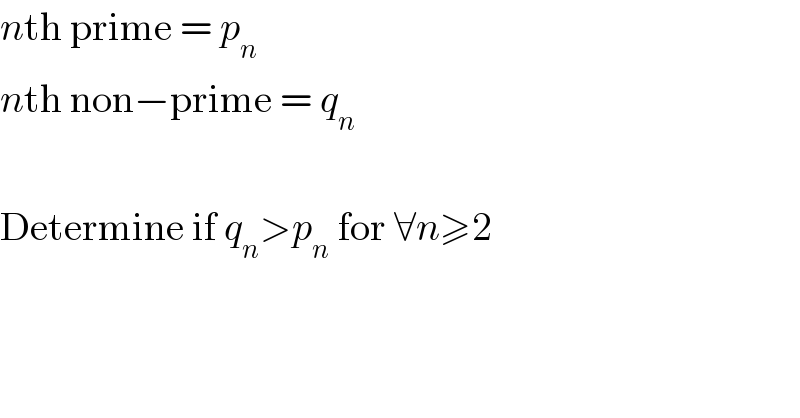
$${n}\mathrm{th}\:\mathrm{prime}\:=\:{p}_{{n}} \\ $$ $${n}\mathrm{th}\:\mathrm{non}−\mathrm{prime}\:=\:{q}_{{n}} \\ $$ $$\: \\ $$ $$\mathrm{Determine}\:\mathrm{if}\:{q}_{{n}} >{p}_{{n}} \:\mathrm{for}\:\forall{n}\geqslant\mathrm{2} \\ $$
Commented byFilupS last updated on 22/Feb/17
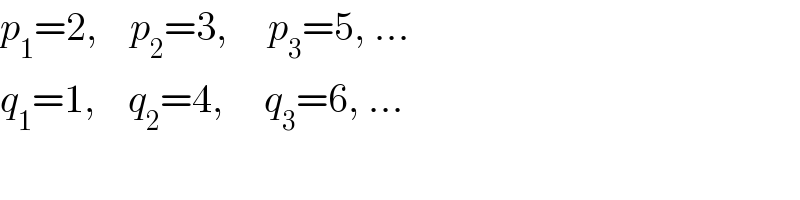
$${p}_{\mathrm{1}} =\mathrm{2},\:\:\:\:{p}_{\mathrm{2}} =\mathrm{3},\:\:\:\:\:{p}_{\mathrm{3}} =\mathrm{5},\:... \\ $$ $${q}_{\mathrm{1}} =\mathrm{1},\:\:\:\:{q}_{\mathrm{2}} =\mathrm{4},\:\:\:\:\:{q}_{\mathrm{3}} =\mathrm{6},\:... \\ $$
Commented bysandy_suhendra last updated on 22/Feb/17
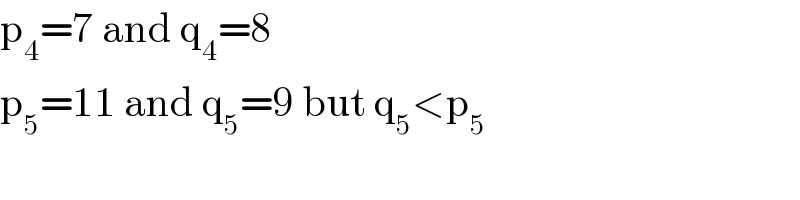
$$\mathrm{p}_{\mathrm{4}} =\mathrm{7}\:\mathrm{and}\:\mathrm{q}_{\mathrm{4}} =\mathrm{8} \\ $$ $$\mathrm{p}_{\mathrm{5}} =\mathrm{11}\:\mathrm{and}\:\mathrm{q}_{\mathrm{5}} =\mathrm{9}\:\mathrm{but}\:\mathrm{q}_{\mathrm{5}} <\mathrm{p}_{\mathrm{5}} \: \\ $$
