
Question Number 106364 by Study last updated on 04/Aug/20

$$\mathrm{0}^{{i}} =????? \\ $$
Commented by Study last updated on 04/Aug/20

$${help}\:{me} \\ $$
Commented by Dwaipayan Shikari last updated on 04/Aug/20

$${Undefined} \\ $$
Answered by mathmax by abdo last updated on 04/Aug/20
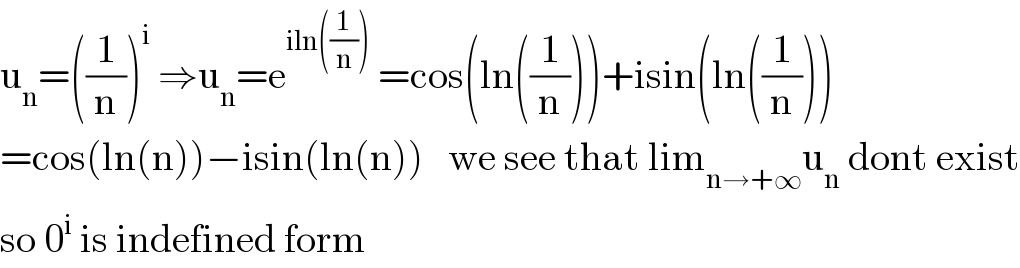
$$\mathrm{u}_{\mathrm{n}} =\left(\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{i}} \:\Rightarrow\mathrm{u}_{\mathrm{n}} =\mathrm{e}^{\mathrm{iln}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)} \:=\mathrm{cos}\left(\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right)+\mathrm{isin}\left(\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right) \\ $$$$=\mathrm{cos}\left(\mathrm{ln}\left(\mathrm{n}\right)\right)−\mathrm{isin}\left(\mathrm{ln}\left(\mathrm{n}\right)\right)\:\:\:\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{u}_{\mathrm{n}} \:\mathrm{dont}\:\mathrm{exist} \\ $$$$\mathrm{so}\:\mathrm{0}^{\mathrm{i}} \:\mathrm{is}\:\mathrm{indefined}\:\mathrm{form} \\ $$
