
Question Number 106313 by bemath last updated on 04/Aug/20

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{x}\mid\mathrm{x}−\mathrm{1}\mid}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Aug/20
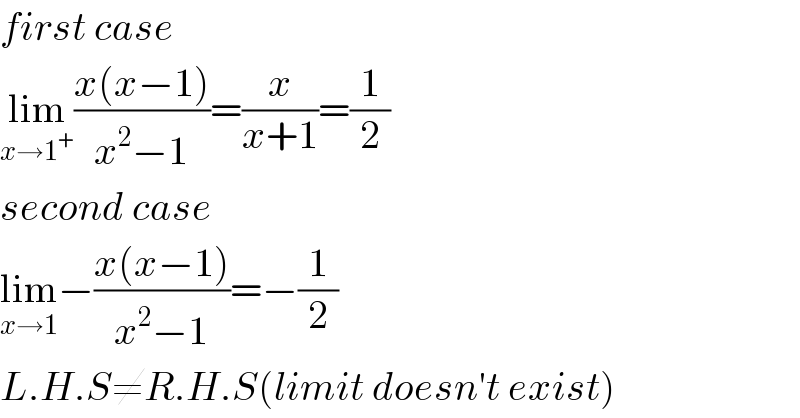
$${first}\:{case} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}\frac{{x}\left({x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}=\frac{{x}}{{x}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${second}\:{case} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−\frac{{x}\left({x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${L}.{H}.{S}\neq{R}.{H}.{S}\left({limit}\:{doesn}'{t}\:{exist}\right) \\ $$
