Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 106281 by bemath last updated on 04/Aug/20

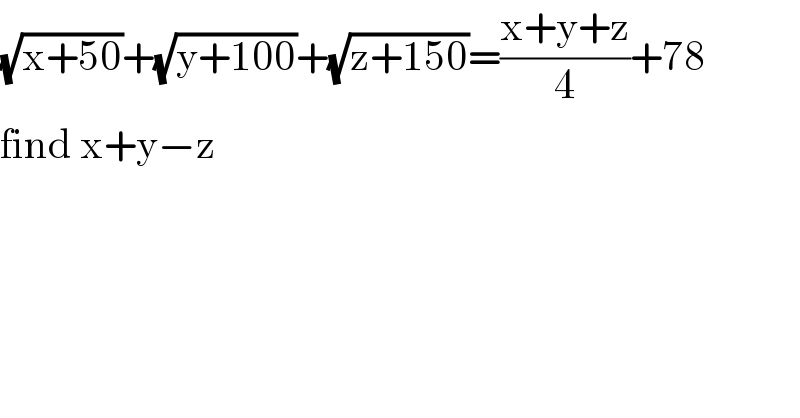
(√(x+50))+(√(y+100))+(√(z+150))=((x+y+z)/4)+78 find x+y−z

$$\sqrt{\mathrm{x}+\mathrm{50}}+\sqrt{\mathrm{y}+\mathrm{100}}+\sqrt{\mathrm{z}+\mathrm{150}}=\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{\mathrm{4}}+\mathrm{78} \\ $$$$\mathrm{find}\:\mathrm{x}+\mathrm{y}−\mathrm{z}\: \\ $$

Answered by bobhans last updated on 04/Aug/20

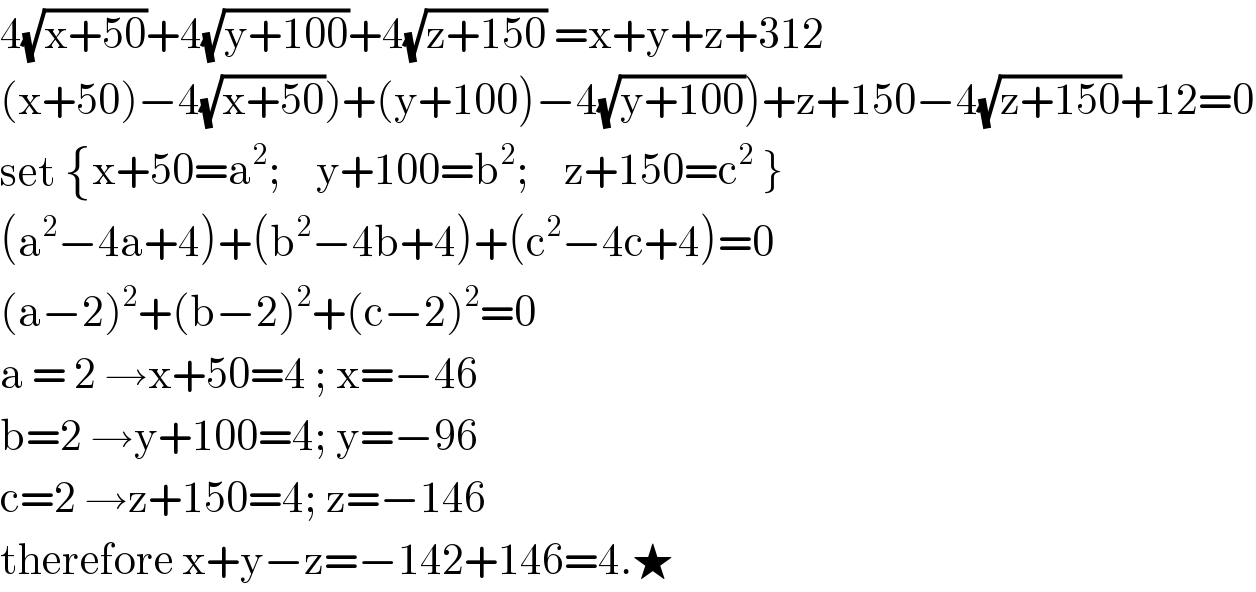
4(√(x+50))+4(√(y+100))+4(√(z+150)) =x+y+z+312 (x+50)−4(√(x+50)))+(y+100)−4(√(y+100)))+z+150−4(√(z+150))+12=0 set { ((x+50=a^2 ;),(y+100=b^2 ;),(z+150=c^2 })) :} (a^2 −4a+4)+(b^2 −4b+4)+(c^2 −4c+4)=0 (a−2)^2 +(b−2)^2 +(c−2)^2 =0 a = 2 →x+50=4 ; x=−46 b=2 →y+100=4; y=−96 c=2 →z+150=4; z=−146 therefore x+y−z=−142+146=4.★

$$\mathrm{4}\sqrt{\mathrm{x}+\mathrm{50}}+\mathrm{4}\sqrt{\mathrm{y}+\mathrm{100}}+\mathrm{4}\sqrt{\mathrm{z}+\mathrm{150}}\:=\mathrm{x}+\mathrm{y}+\mathrm{z}+\mathrm{312} \\ $$$$\left.\left(\left.\mathrm{x}+\mathrm{50}\right)−\mathrm{4}\sqrt{\mathrm{x}+\mathrm{50}}\right)+\left(\mathrm{y}+\mathrm{100}\right)−\mathrm{4}\sqrt{\mathrm{y}+\mathrm{100}}\right)+\mathrm{z}+\mathrm{150}−\mathrm{4}\sqrt{\mathrm{z}+\mathrm{150}}+\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{set}\:\begin{cases}{\mathrm{x}+\mathrm{50}=\mathrm{a}^{\mathrm{2}} ;}&{\mathrm{y}+\mathrm{100}=\mathrm{b}^{\mathrm{2}} ;}&{\left.\mathrm{z}+\mathrm{150}=\mathrm{c}^{\mathrm{2}} \:\right\}}\end{cases} \\ $$$$\left(\mathrm{a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{4}\right)+\left(\mathrm{b}^{\mathrm{2}} −\mathrm{4b}+\mathrm{4}\right)+\left(\mathrm{c}^{\mathrm{2}} −\mathrm{4c}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\left(\mathrm{a}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{b}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{c}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{a}\:=\:\mathrm{2}\:\rightarrow\mathrm{x}+\mathrm{50}=\mathrm{4}\:;\:\mathrm{x}=−\mathrm{46} \\ $$$$\mathrm{b}=\mathrm{2}\:\rightarrow\mathrm{y}+\mathrm{100}=\mathrm{4};\:\mathrm{y}=−\mathrm{96} \\ $$$$\mathrm{c}=\mathrm{2}\:\rightarrow\mathrm{z}+\mathrm{150}=\mathrm{4};\:\mathrm{z}=−\mathrm{146} \\ $$$$\mathrm{therefore}\:\mathrm{x}+\mathrm{y}−\mathrm{z}=−\mathrm{142}+\mathrm{146}=\mathrm{4}.\bigstar \\ $$

Commented by bemath last updated on 04/Aug/20

waw....super..

$$\mathrm{waw}....\mathrm{super}.. \\ $$

Answered by john santu last updated on 04/Aug/20

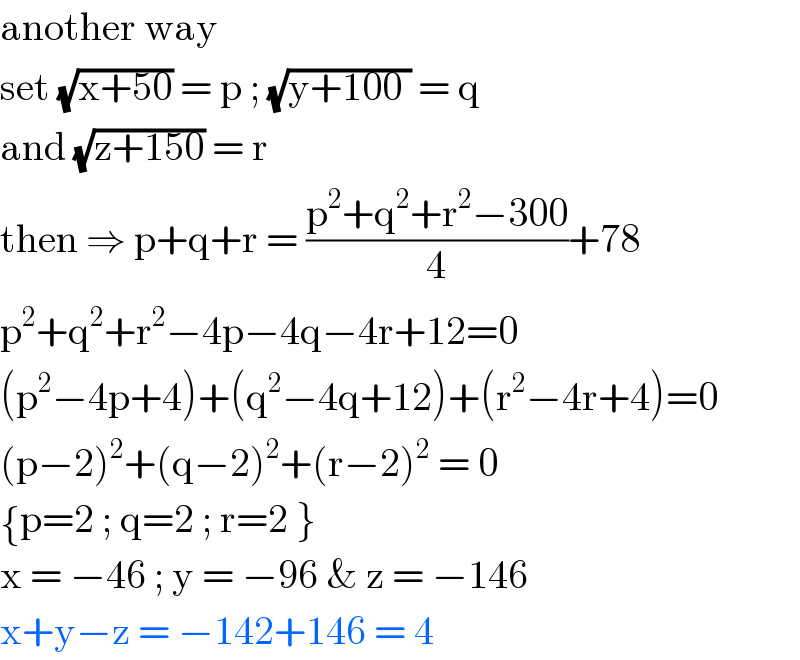
another way set (√(x+50)) = p ; (√(y+100 )) = q and (√(z+150)) = r then ⇒ p+q+r = ((p^2 +q^2 +r^2 −300)/4)+78 p^2 +q^2 +r^2 −4p−4q−4r+12=0 (p^2 −4p+4)+(q^2 −4q+12)+(r^2 −4r+4)=0 (p−2)^2 +(q−2)^2 +(r−2)^2 = 0 { ((p=2 ; q=2 ; r=2 })) :} x = −46 ; y = −96 & z = −146 x+y−z = −142+146 = 4

$$\mathrm{another}\:\mathrm{way}\: \\ $$$$\mathrm{set}\:\sqrt{\mathrm{x}+\mathrm{50}}\:=\:\mathrm{p}\:;\:\sqrt{\mathrm{y}+\mathrm{100}\:}\:=\:\mathrm{q} \\ $$$$\mathrm{and}\:\sqrt{\mathrm{z}+\mathrm{150}}\:=\:\mathrm{r}\: \\ $$$$\mathrm{then}\:\Rightarrow\:\mathrm{p}+\mathrm{q}+\mathrm{r}\:=\:\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} −\mathrm{300}}{\mathrm{4}}+\mathrm{78} \\ $$$$\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} −\mathrm{4p}−\mathrm{4q}−\mathrm{4r}+\mathrm{12}=\mathrm{0} \\ $$$$\left(\mathrm{p}^{\mathrm{2}} −\mathrm{4p}+\mathrm{4}\right)+\left(\mathrm{q}^{\mathrm{2}} −\mathrm{4q}+\mathrm{12}\right)+\left(\mathrm{r}^{\mathrm{2}} −\mathrm{4r}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\left(\mathrm{p}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{q}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{r}−\mathrm{2}\right)^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\begin{cases}{\left.\mathrm{p}=\mathrm{2}\:;\:\mathrm{q}=\mathrm{2}\:;\:\mathrm{r}=\mathrm{2}\:\right\}}\end{cases} \\ $$$$\mathrm{x}\:=\:−\mathrm{46}\:;\:\mathrm{y}\:=\:−\mathrm{96}\:\&\:\mathrm{z}\:=\:−\mathrm{146}\: \\ $$$$\mathrm{x}+\mathrm{y}−\mathrm{z}\:=\:−\mathrm{142}+\mathrm{146}\:=\:\mathrm{4}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com