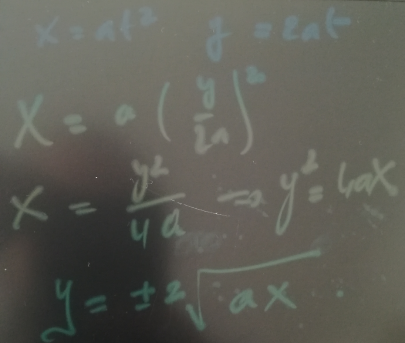Question Number 106167 by mohammad17 last updated on 03/Aug/20

Answered by bemath last updated on 03/Aug/20
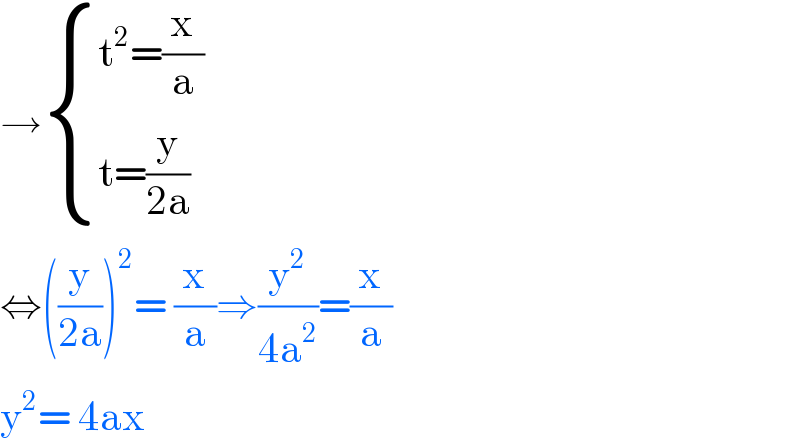
$$\rightarrow\begin{cases}{\mathrm{t}^{\mathrm{2}} =\frac{\mathrm{x}}{\mathrm{a}}}\\{\mathrm{t}=\frac{\mathrm{y}}{\mathrm{2a}}}\end{cases} \\ $$$$\Leftrightarrow\left(\frac{\mathrm{y}}{\mathrm{2a}}\right)^{\mathrm{2}} =\:\frac{\mathrm{x}}{\mathrm{a}}\Rightarrow\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{4a}^{\mathrm{2}} }=\frac{\mathrm{x}}{\mathrm{a}} \\ $$$$\mathrm{y}^{\mathrm{2}} =\:\mathrm{4ax}\: \\ $$
Commented by mohammad17 last updated on 03/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Aziztisffola last updated on 03/Aug/20