
Question Number 106125 by Ar Brandon last updated on 02/Aug/20
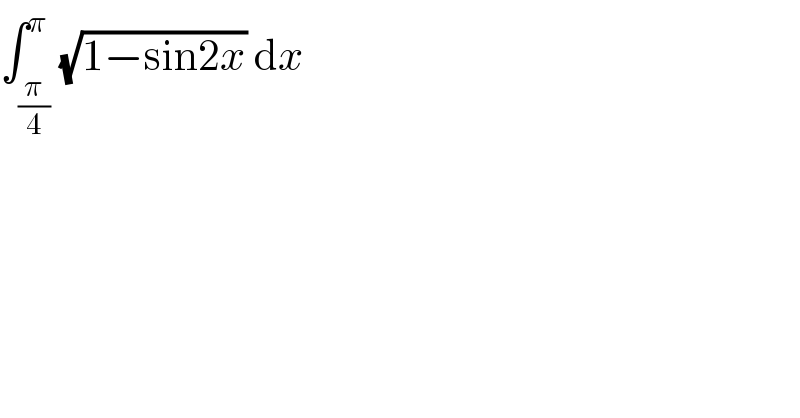
$$\int_{\frac{\pi}{\mathrm{4}}} ^{\pi} \sqrt{\mathrm{1}−\mathrm{sin2}{x}}\:\mathrm{d}{x} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Aug/20
![∫_(π/4) ^π sinx−cosx dx or∫_(π/4) ^π cosx−sinx −[(sinx+cosx)]_(π/4) ^π =1+(√2) or∫_(π/4) ^π cosx−sinx= [sinx+cosx]_(π/4) ^π =−(1+(√2))](Q106127.png)
$$\int_{\frac{\pi}{\mathrm{4}}} ^{\pi} \mathrm{sinx}−\mathrm{cosx}\:\mathrm{dx}\:\:\:\:\:\mathrm{or}\int_{\frac{\pi}{\mathrm{4}}} ^{\pi} \mathrm{cosx}−\mathrm{sinx} \\ $$$$−\left[\left(\mathrm{sinx}+\mathrm{cosx}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\pi} =\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{or}\int_{\frac{\pi}{\mathrm{4}}} ^{\pi} \mathrm{cosx}−\mathrm{sinx}=\:\:\left[\mathrm{sinx}+\mathrm{cosx}\right]_{\frac{\pi}{\mathrm{4}}} ^{\pi} =−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Commented by Ar Brandon last updated on 02/Aug/20
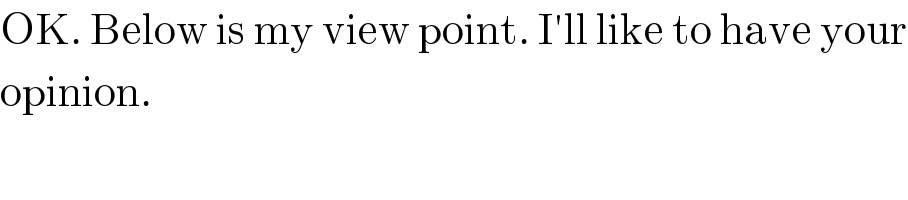
$$\mathrm{OK}.\:\mathrm{Below}\:\mathrm{is}\:\mathrm{my}\:\mathrm{view}\:\mathrm{point}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{like}\:\mathrm{to}\:\mathrm{have}\:\mathrm{your} \\ $$$$\mathrm{opinion}. \\ $$
Answered by Ar Brandon last updated on 02/Aug/20
![f(x)=(√(1−sin2x))=(√((cosx−sinx)^2 )) =∣cosx−sinx∣=(√2)∣cos(x+(π/4))∣ f(x)= { (((√2)cos(x+(π/4)) for −(3/4)≤x≤(π/4))),((−(√2)cos(x+(π/4)) for (π/4)<x<((5π)/4))) :} ⇒∫_(π/4) ^π f(x)dx=−(√2)∫_(π/4) ^π cos(x+(π/4))dx =−(√2)[sin(x+(π/4))]_(π/4) ^π =−(√2)(−(1/(√2))−1) =(√2)+1](Q106128.png)
$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{1}−\mathrm{sin2x}}=\sqrt{\left(\mathrm{cosx}−\mathrm{sinx}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:=\mid\mathrm{cosx}−\mathrm{sinx}\mid=\sqrt{\mathrm{2}}\mid\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mid \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\begin{cases}{\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\:\:\:\mathrm{for}\:−\frac{\mathrm{3}}{\mathrm{4}}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{4}}}\\{−\sqrt{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\:\mathrm{for}\:\frac{\pi}{\mathrm{4}}<\mathrm{x}<\frac{\mathrm{5}\pi}{\mathrm{4}}}\end{cases} \\ $$$$\Rightarrow\int_{\frac{\pi}{\mathrm{4}}} ^{\pi} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=−\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{\pi} \mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\sqrt{\mathrm{2}}\left[\mathrm{sin}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\right]_{\frac{\pi}{\mathrm{4}}} ^{\pi} =−\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}}+\mathrm{1} \\ $$
Commented by 1549442205PVT last updated on 03/Aug/20
![By the hypothesis the interval to take integration be [(π/4);π],so (π/2)≤(π/4)+x≤((5π)/4) ⇒cos((π/4)+x)<0](Q106136.png)
$$\mathrm{By}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{the}\:\mathrm{interval}\:\mathrm{to}\:\mathrm{take} \\ $$$$\mathrm{integration}\:\mathrm{be}\:\left[\frac{\pi}{\mathrm{4}};\pi\right],\mathrm{so}\:\frac{\pi}{\mathrm{2}}\leqslant\frac{\pi}{\mathrm{4}}+\mathrm{x}\leqslant\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}+\mathrm{x}\right)<\mathrm{0} \\ $$
