
Question Number 106076 by Skabetix last updated on 02/Aug/20

$${solve}\:{this}\:{pls} \\ $$$${x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } =\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Aug/20
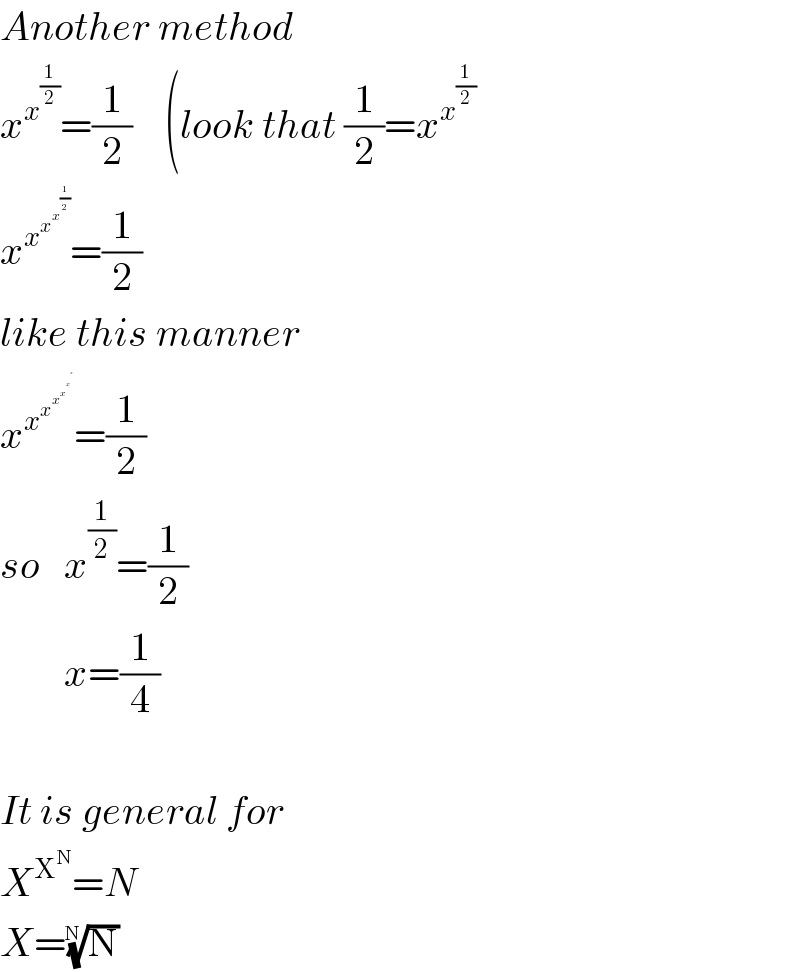
$${Another}\:{method} \\ $$$${x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } =\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\left({look}\:{that}\:\frac{\mathrm{1}}{\mathrm{2}}={x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } \right. \\ $$$${x}^{{x}^{{x}^{{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } } } =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${like}\:{this}\:{manner} \\ $$$${x}^{{x}^{{x}^{{x}^{{x}^{{x}^{{x}} } } } } } =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${so}\:\:\:{x}^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$$${It}\:{is}\:{general}\:{for}\: \\ $$$${X}^{\mathrm{X}^{\mathrm{N}} } ={N} \\ $$$${X}=\sqrt[{\mathrm{N}}]{\mathrm{N}} \\ $$
Commented by mr W last updated on 02/Aug/20
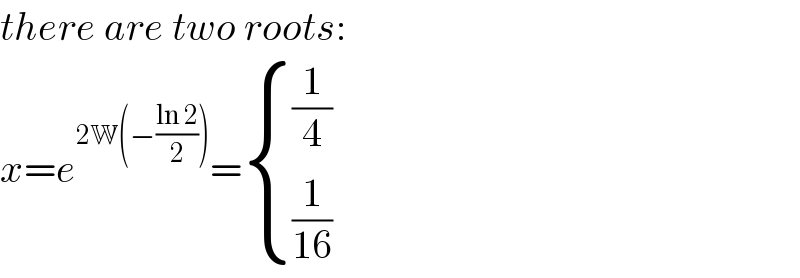
$${there}\:{are}\:{two}\:{roots}: \\ $$$${x}={e}^{\mathrm{2}\mathbb{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}\right)} =\begin{cases}{\frac{\mathrm{1}}{\mathrm{4}}}\\{\frac{\mathrm{1}}{\mathrm{16}}}\end{cases} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Aug/20
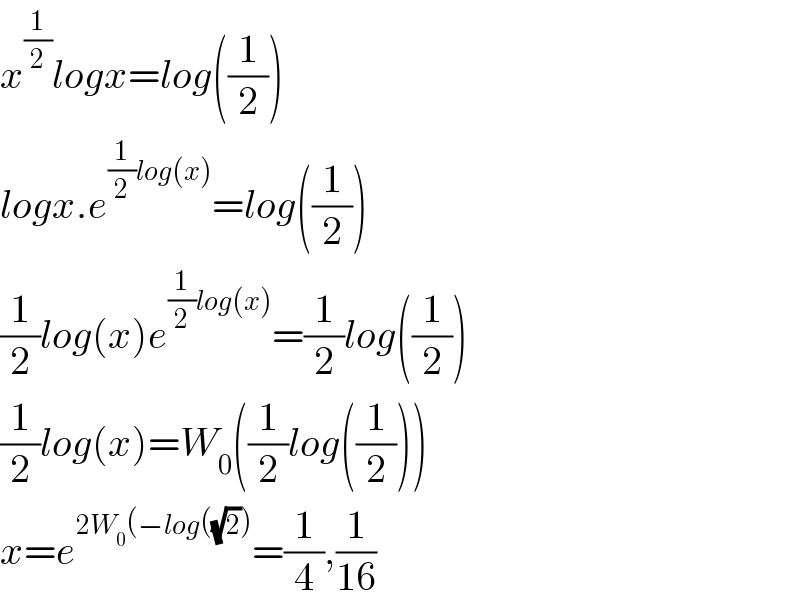
$${x}^{\frac{\mathrm{1}}{\mathrm{2}}} {logx}={log}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${logx}.{e}^{\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}\right)} ={log}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}\right){e}^{\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}\right)} =\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}\right)={W}_{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$${x}={e}^{\mathrm{2}{W}_{\mathrm{0}} \left(−{log}\left(\sqrt{\mathrm{2}}\right)\right.} =\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{16}} \\ $$
