
Question Number 106072 by bemath last updated on 02/Aug/20
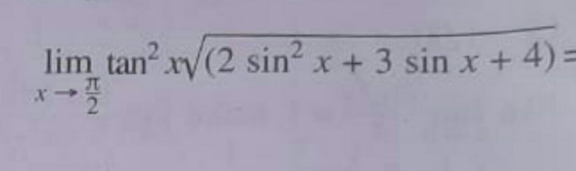
Answered by bobhans last updated on 02/Aug/20
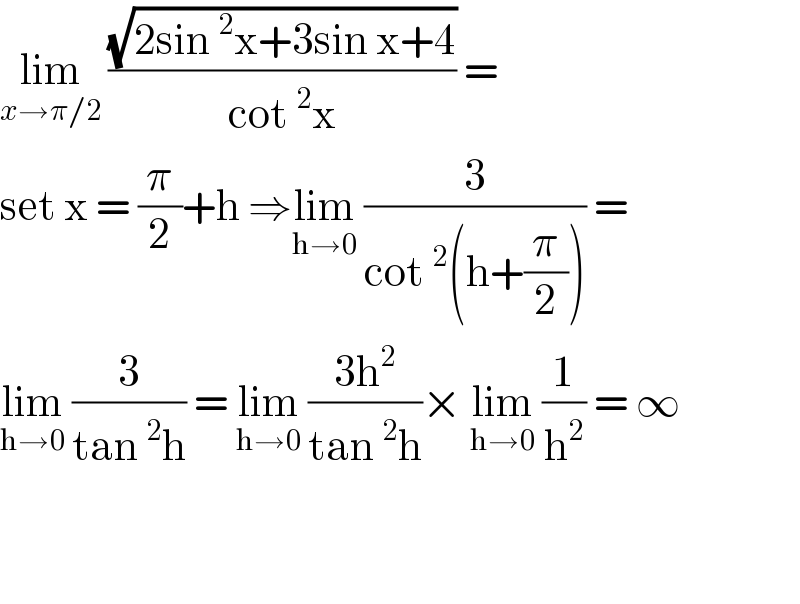
$$\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}+\mathrm{4}}}{\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}}\:= \\ $$$$\mathrm{set}\:\mathrm{x}\:=\:\frac{\pi}{\mathrm{2}}+\mathrm{h}\:\Rightarrow\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}}{\mathrm{cot}\:^{\mathrm{2}} \left(\mathrm{h}+\frac{\pi}{\mathrm{2}}\right)}\:= \\ $$$$\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{h}}\:=\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3h}^{\mathrm{2}} }{\mathrm{tan}\:^{\mathrm{2}} \mathrm{h}}×\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{h}^{\mathrm{2}} }\:=\:\infty\: \\ $$$$ \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 02/Aug/20
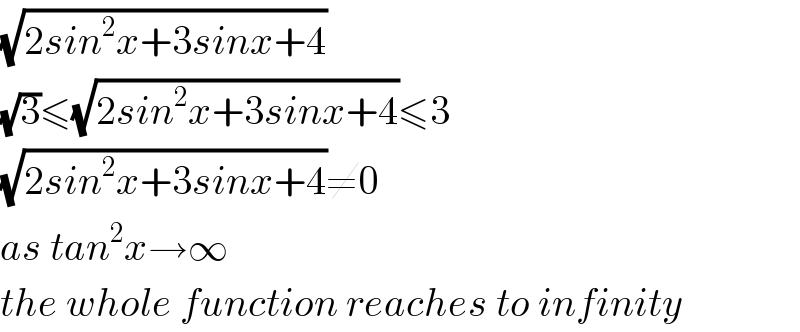
$$\sqrt{\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{3}{sinx}+\mathrm{4}} \\ $$$$\sqrt{\mathrm{3}}\leqslant\sqrt{\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{3}{sinx}+\mathrm{4}}\leqslant\mathrm{3} \\ $$$$\sqrt{\mathrm{2}{sin}^{\mathrm{2}} {x}+\mathrm{3}{sinx}+\mathrm{4}}\neq\mathrm{0} \\ $$$${as}\:{tan}^{\mathrm{2}} {x}\rightarrow\infty \\ $$$${the}\:{whole}\:{function}\:{reaches}\:{to}\:{infinity} \\ $$
