Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 106005 by bemath last updated on 02/Aug/20

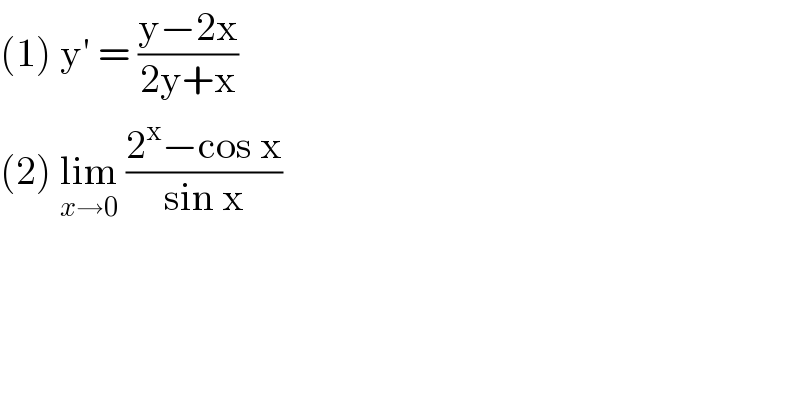
(1) y′ = ((y−2x)/(2y+x)) (2) lim_(x→0) ((2^x −cos x)/(sin x))

$$\left(\mathrm{1}\right)\:\mathrm{y}'\:=\:\frac{\mathrm{y}−\mathrm{2x}}{\mathrm{2y}+\mathrm{x}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}^{\mathrm{x}} −\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}} \\ $$

Answered by bobhans last updated on 02/Aug/20

(1) (dy/dx) = ((y−2x)/(2y+x)) [ set y = ♭x ] (dy/dx) = ♭ + x (d♭/dx) ⇒ ♭+x (d♭/dx) = ((♭x−2x)/(2♭x+x)) ♭ + x (d♭/dx) = ((♭−2)/(2♭+1))→x (d♭/dx) = ((♭−2−♭(2♭+1))/(2♭+1)) x (d♭/dx) = ((−2♭^2 −2)/(2♭+1)) → ((2♭+1)/(♭^2 +1)) d♭ = −2(dx/x) ∫ ((2♭)/(♭^2 +1))d♭+∫ (d♭/(♭^2 +1)) = −ln x^2 + c ∫ ((d(♭^2 +1))/(♭^2 +1))+ arc tan (♭) = ln ∣(C/x^2 )∣ ln ∣♭^2 +1∣+arc tan (♭) = ln ∣(C/x^2 )∣ arc tan (♭) = ln ∣(C/(x^2 (♭^2 +1)))∣ ⇔ arc tan ((y/x)) = ln ∣(C/(x^2 (((y^2 +x^2 )/x^2 ))))∣ arc tan ((y/x)) = ln ∣(C/(y^2 +x^2 ))∣ ★

$$\left(\mathrm{1}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{y}−\mathrm{2x}}{\mathrm{2y}+\mathrm{x}}\:\:\left[\:\mathrm{set}\:\mathrm{y}\:=\:\flat\mathrm{x}\:\right]\: \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\flat\:+\:\mathrm{x}\:\frac{\mathrm{d}\flat}{\mathrm{dx}}\:\Rightarrow\:\flat+\mathrm{x}\:\frac{\mathrm{d}\flat}{\mathrm{dx}}\:=\:\frac{\flat\mathrm{x}−\mathrm{2x}}{\mathrm{2}\flat\mathrm{x}+\mathrm{x}} \\ $$$$\flat\:+\:\mathrm{x}\:\frac{\mathrm{d}\flat}{\mathrm{dx}}\:=\:\frac{\flat−\mathrm{2}}{\mathrm{2}\flat+\mathrm{1}}\rightarrow\mathrm{x}\:\frac{\mathrm{d}\flat}{\mathrm{dx}}\:=\:\frac{\flat−\mathrm{2}−\flat\left(\mathrm{2}\flat+\mathrm{1}\right)}{\mathrm{2}\flat+\mathrm{1}} \\ $$$$\mathrm{x}\:\frac{\mathrm{d}\flat}{\mathrm{dx}}\:=\:\frac{−\mathrm{2}\flat^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}\flat+\mathrm{1}}\:\rightarrow\:\frac{\mathrm{2}\flat+\mathrm{1}}{\flat^{\mathrm{2}} +\mathrm{1}}\:\mathrm{d}\flat\:=\:−\mathrm{2}\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$\int\:\frac{\mathrm{2}\flat}{\flat^{\mathrm{2}} +\mathrm{1}}\mathrm{d}\flat+\int\:\frac{\mathrm{d}\flat}{\flat^{\mathrm{2}} +\mathrm{1}}\:=\:−\mathrm{ln}\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{c} \\ $$$$\int\:\frac{\mathrm{d}\left(\flat^{\mathrm{2}} +\mathrm{1}\right)}{\flat^{\mathrm{2}} +\mathrm{1}}+\:\mathrm{arc}\:\mathrm{tan}\:\left(\flat\right)\:=\:\mathrm{ln}\:\mid\frac{\mathrm{C}}{\mathrm{x}^{\mathrm{2}} }\mid \\ $$$$\mathrm{ln}\:\mid\flat^{\mathrm{2}} +\mathrm{1}\mid+\mathrm{arc}\:\mathrm{tan}\:\left(\flat\right)\:=\:\mathrm{ln}\:\mid\frac{\mathrm{C}}{\mathrm{x}^{\mathrm{2}} }\mid \\ $$$$\mathrm{arc}\:\mathrm{tan}\:\left(\flat\right)\:\:=\:\mathrm{ln}\:\mid\frac{\mathrm{C}}{\mathrm{x}^{\mathrm{2}} \left(\flat^{\mathrm{2}} +\mathrm{1}\right)}\mid \\ $$$$\Leftrightarrow\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\:=\:\mathrm{ln}\:\mid\frac{\mathrm{C}}{\mathrm{x}^{\mathrm{2}} \left(\frac{\mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\right)}\mid\: \\ $$$$\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{y}}{\mathrm{x}}\right)\:=\:\mathrm{ln}\:\mid\frac{\mathrm{C}}{\mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }\mid\:\bigstar \\ $$

Commented by bemath last updated on 02/Aug/20

typo in part ((2♭+1)/(♭^2 +1))

$$\mathrm{typo}\:\mathrm{in}\:\mathrm{part}\:\frac{\mathrm{2}\flat+\mathrm{1}}{\flat^{\mathrm{2}} +\mathrm{1}} \\ $$

Answered by bobhans last updated on 02/Aug/20

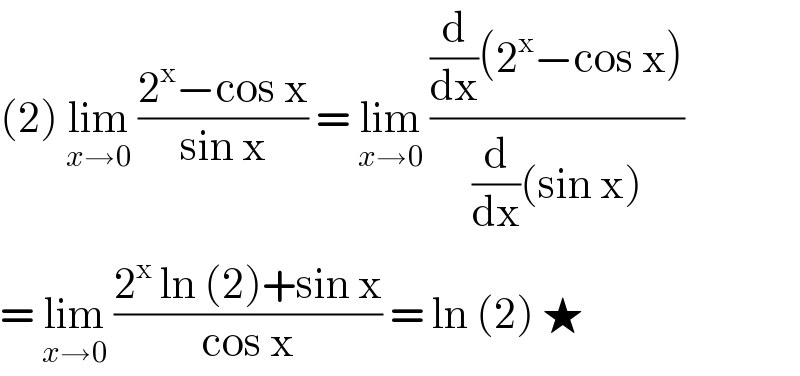
(2) lim_(x→0) ((2^x −cos x)/(sin x)) = lim_(x→0) (((d/dx)(2^x −cos x))/((d/dx)(sin x))) = lim_(x→0) ((2^x ln (2)+sin x)/(cos x)) = ln (2) ★

$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}^{\mathrm{x}} −\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{2}^{\mathrm{x}} −\mathrm{cos}\:\mathrm{x}\right)}{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{sin}\:\mathrm{x}\right)} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}^{\mathrm{x}} \:\mathrm{ln}\:\left(\mathrm{2}\right)+\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}\:=\:\mathrm{ln}\:\left(\mathrm{2}\right)\:\bigstar \\ $$

Answered by Dwaipayan Shikari last updated on 02/Aug/20

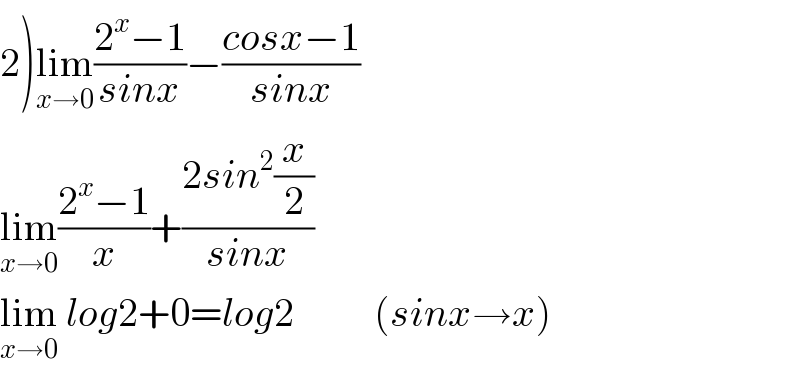
2)lim_(x→0) ((2^x −1)/(sinx))−((cosx−1)/(sinx)) lim_(x→0) ((2^x −1)/x)+((2sin^2 (x/2))/(sinx)) lim_(x→0) log2+0=log2 (sinx→x)

$$\left.\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}^{{x}} −\mathrm{1}}{{sinx}}−\frac{{cosx}−\mathrm{1}}{{sinx}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}^{{x}} −\mathrm{1}}{{x}}+\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{sinx}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{log}\mathrm{2}+\mathrm{0}={log}\mathrm{2}\:\:\:\:\:\:\:\:\:\:\left({sinx}\rightarrow{x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com