
Question Number 105969 by Ar Brandon last updated on 02/Aug/20
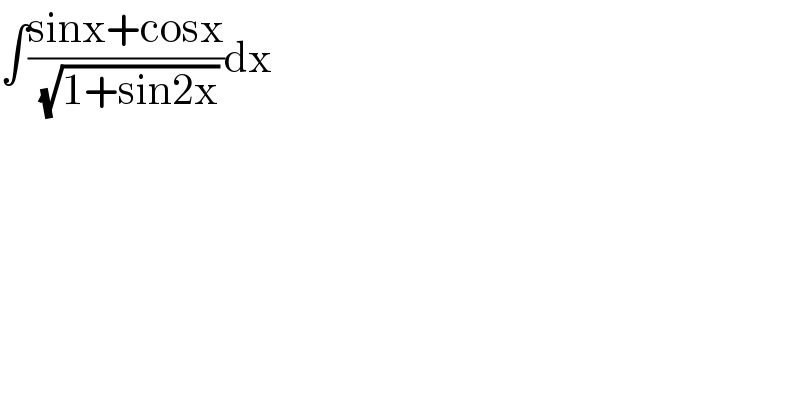
$$\int\frac{\mathrm{sinx}+\mathrm{cosx}}{\sqrt{\mathrm{1}+\mathrm{sin2x}}}\mathrm{dx} \\ $$
Answered by bobhans last updated on 02/Aug/20
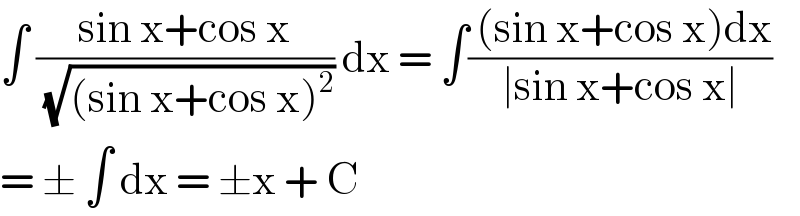
$$\int\:\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\sqrt{\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} }}\:\mathrm{dx}\:=\:\int\frac{\:\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)\mathrm{dx}}{\mid\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\mid} \\ $$$$=\:\pm\:\int\:\mathrm{dx}\:=\:\pm\mathrm{x}\:+\:\mathrm{C} \\ $$
Commented by Ar Brandon last updated on 02/Aug/20
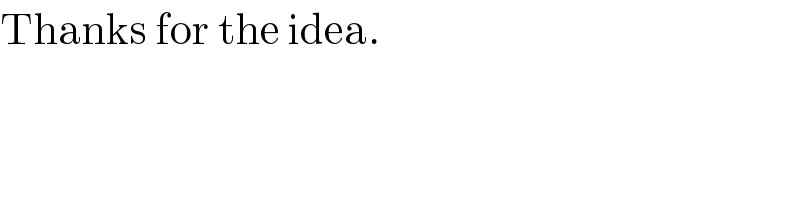
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{idea}. \\ $$
Commented by bobhans last updated on 02/Aug/20

$$\mathrm{sorry}\:\mathrm{typo} \\ $$
Commented by malwaan last updated on 02/Aug/20
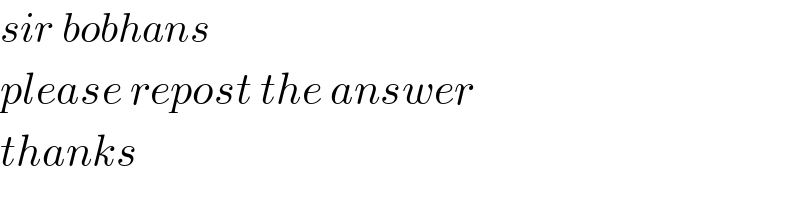
$${sir}\:{bobhans} \\ $$$${please}\:{repost}\:{the}\:{answer} \\ $$$${thanks} \\ $$
Answered by Ar Brandon last updated on 02/Aug/20
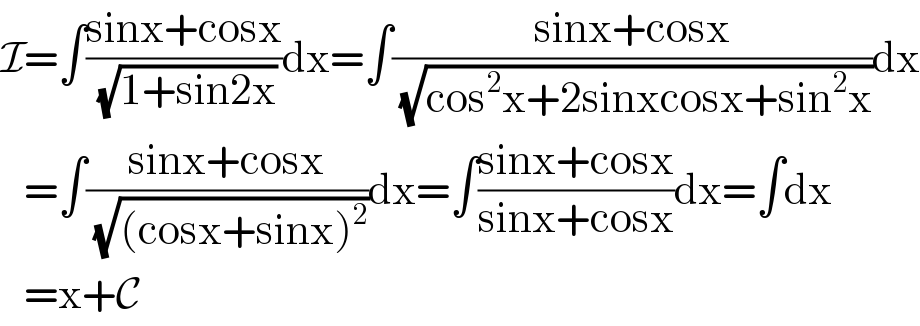
$$\mathcal{I}=\int\frac{\mathrm{sinx}+\mathrm{cosx}}{\sqrt{\mathrm{1}+\mathrm{sin2x}}}\mathrm{dx}=\int\frac{\mathrm{sinx}+\mathrm{cosx}}{\sqrt{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{2sinxcosx}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}}\mathrm{dx} \\ $$$$\:\:\:=\int\frac{\mathrm{sinx}+\mathrm{cosx}}{\sqrt{\left(\mathrm{cosx}+\mathrm{sinx}\right)^{\mathrm{2}} }}\mathrm{dx}=\int\frac{\mathrm{sinx}+\mathrm{cosx}}{\mathrm{sinx}+\mathrm{cosx}}\mathrm{dx}=\int\mathrm{dx} \\ $$$$\:\:\:=\mathrm{x}+\mathcal{C} \\ $$
Commented by prakash jain last updated on 02/Aug/20
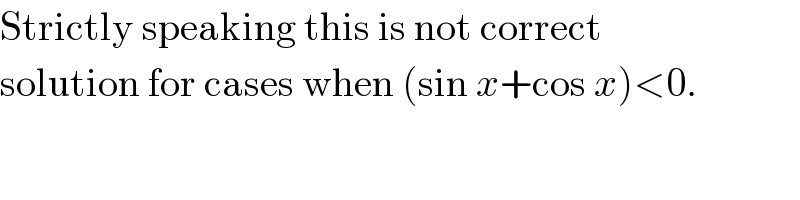
$$\mathrm{Strictly}\:\mathrm{speaking}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct} \\ $$$$\mathrm{solution}\:\mathrm{for}\:\mathrm{cases}\:\mathrm{when}\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)<\mathrm{0}. \\ $$
Commented by Ar Brandon last updated on 02/Aug/20
OK Sir, thanks. I didn't take that into consideration. You're right.
Answered by bemath last updated on 02/Aug/20
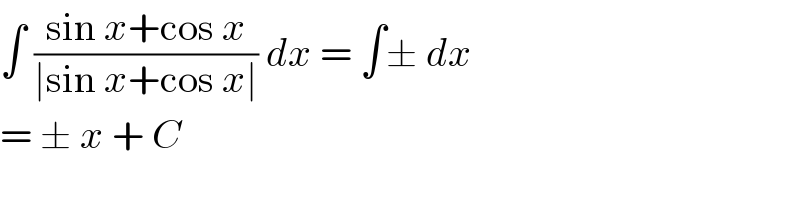
$$\int\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mid\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\mid}\:{dx}\:=\:\int\pm\:{dx}\: \\ $$$$=\:\pm\:{x}\:+\:{C} \\ $$
Commented by prakash jain last updated on 02/Aug/20
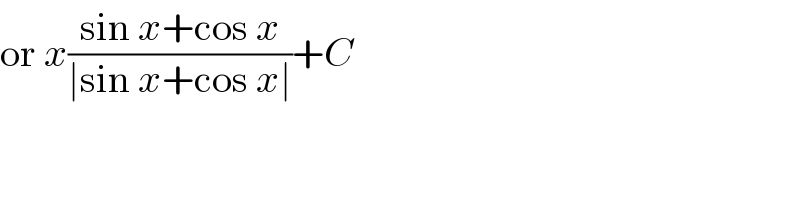
$$\mathrm{or}\:{x}\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mid\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\mid}+{C} \\ $$
Commented by 1549442205PVT last updated on 02/Aug/20
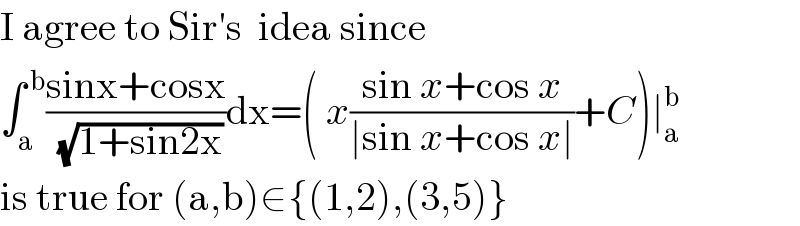
$$\mathrm{I}\:\mathrm{agree}\:\mathrm{to}\:\mathrm{Sir}'\mathrm{s}\:\:\mathrm{idea}\:\mathrm{since}\: \\ $$$$\int_{\mathrm{a}} ^{\:\mathrm{b}} \frac{\mathrm{sinx}+\mathrm{cosx}}{\sqrt{\mathrm{1}+\mathrm{sin2x}}}\mathrm{dx}=\left(\:{x}\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mid\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\mid}+{C}\right)\mid_{\mathrm{a}} ^{\mathrm{b}} \\ $$$$\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\left(\mathrm{a},\mathrm{b}\right)\in\left\{\left(\mathrm{1},\mathrm{2}\right),\left(\mathrm{3},\mathrm{5}\right)\right\} \\ $$
