
Question Number 105916 by bobhans last updated on 02/Aug/20
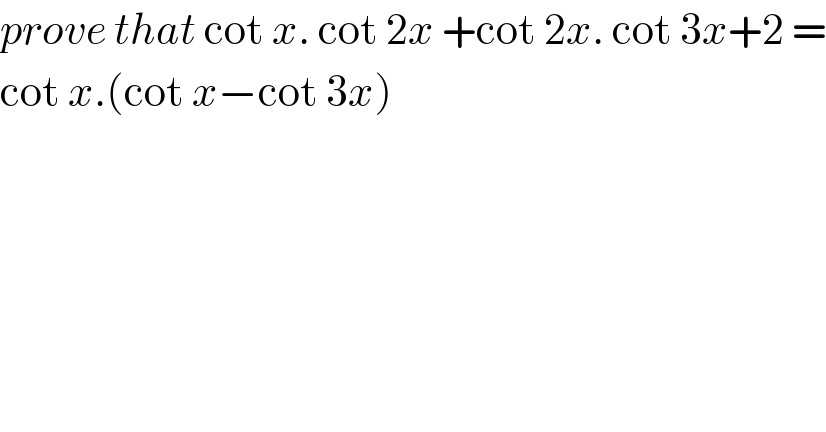
$${prove}\:{that}\:\mathrm{cot}\:{x}.\:\mathrm{cot}\:\mathrm{2}{x}\:+\mathrm{cot}\:\mathrm{2}{x}.\:\mathrm{cot}\:\mathrm{3}{x}+\mathrm{2}\:= \\ $$$$\mathrm{cot}\:{x}.\left(\mathrm{cot}\:{x}−\mathrm{cot}\:\mathrm{3}{x}\right)\: \\ $$
Answered by bemath last updated on 01/Aug/20
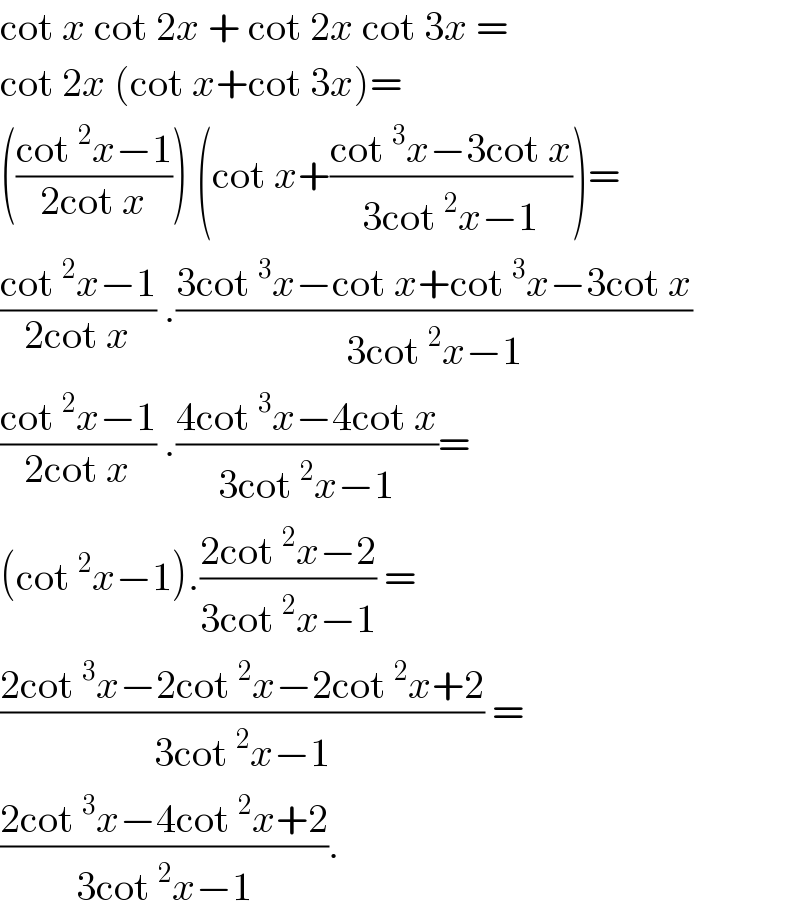
$$\mathrm{cot}\:{x}\:\mathrm{cot}\:\mathrm{2}{x}\:+\:\mathrm{cot}\:\mathrm{2}{x}\:\mathrm{cot}\:\mathrm{3}{x}\:=\: \\ $$$$\mathrm{cot}\:\mathrm{2}{x}\:\left(\mathrm{cot}\:{x}+\mathrm{cot}\:\mathrm{3}{x}\right)= \\ $$$$\left(\frac{\mathrm{cot}\:^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{2cot}\:{x}}\right)\:\left(\mathrm{cot}\:{x}+\frac{\mathrm{cot}\:^{\mathrm{3}} {x}−\mathrm{3cot}\:{x}}{\mathrm{3cot}\:^{\mathrm{2}} {x}−\mathrm{1}}\right)= \\ $$$$\frac{\mathrm{cot}\:^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{2cot}\:{x}}\:.\frac{\mathrm{3cot}\:^{\mathrm{3}} {x}−\mathrm{cot}\:{x}+\mathrm{cot}\:^{\mathrm{3}} {x}−\mathrm{3cot}\:{x}}{\mathrm{3cot}\:^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$\frac{\mathrm{cot}\:^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{2cot}\:{x}}\:.\frac{\mathrm{4cot}\:^{\mathrm{3}} {x}−\mathrm{4cot}\:{x}}{\mathrm{3cot}\:^{\mathrm{2}} {x}−\mathrm{1}}= \\ $$$$\left(\mathrm{cot}\:^{\mathrm{2}} {x}−\mathrm{1}\right).\frac{\mathrm{2cot}\:^{\mathrm{2}} {x}−\mathrm{2}}{\mathrm{3cot}\:^{\mathrm{2}} {x}−\mathrm{1}}\:=\: \\ $$$$\frac{\mathrm{2cot}\:^{\mathrm{3}} {x}−\mathrm{2cot}\:^{\mathrm{2}} {x}−\mathrm{2cot}\:^{\mathrm{2}} {x}+\mathrm{2}}{\mathrm{3cot}\:^{\mathrm{2}} {x}−\mathrm{1}}\:= \\ $$$$\frac{\mathrm{2cot}\:^{\mathrm{3}} {x}−\mathrm{4cot}\:^{\mathrm{2}} {x}+\mathrm{2}}{\mathrm{3cot}\:^{\mathrm{2}} {x}−\mathrm{1}}. \\ $$
Answered by bobhans last updated on 02/Aug/20

$$\mathrm{consider}\:\mathrm{cot}\:\mathrm{2x}\:\mathrm{cot}\:\mathrm{3x}\:+\:\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{3x}\:= \\ $$$$\mathrm{cot}\:\left(\mathrm{2x}+\mathrm{x}\right)\left(\mathrm{cot}\:\mathrm{2x}+\:\mathrm{cot}\:\mathrm{x}\right)= \\ $$$$\frac{\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}−\mathrm{1}}{\mathrm{cot}\:\mathrm{2x}+\mathrm{cot}\:\mathrm{x}}\left(\mathrm{cot}\:\mathrm{2x}+\mathrm{cot}\:\mathrm{x}\right)\:= \\ $$$$\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}−\mathrm{1}\: \\ $$$$\mathrm{adding}\:\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}\:\mathrm{both}\:\mathrm{sides},\: \\ $$$$\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}+\mathrm{cot}\:\mathrm{2x}\:\mathrm{cot}\:\mathrm{3x}\:+\:\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{3x}= \\ $$$$\mathrm{2cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}−\mathrm{1} \\ $$$$\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}\:+\mathrm{cot}\:\mathrm{2x}\:\mathrm{cot}\:\mathrm{3x}+\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{3x}+\mathrm{2}= \\ $$$$\mathrm{2cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}+\mathrm{1} \\ $$$$\therefore\:\mathrm{2}\left(\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}\right)\left(\frac{\mathrm{cos}\:\mathrm{2x}}{\mathrm{sin}\:\mathrm{2x}}\right)+\mathrm{1}=\mathrm{2}\left(\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}\right)\left(\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{2sin}\:\mathrm{xcos}\:\mathrm{x}}\right)+\mathrm{1} \\ $$$$=\:\mathrm{cot}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\therefore\:\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}\:+\:\mathrm{cot}\:\mathrm{2x}\:\mathrm{cot}\:\mathrm{3x}\:=\:\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cot}\:\mathrm{xcot}\:\mathrm{3x} \\ $$$$\mathrm{cot}\:\mathrm{x}\:\mathrm{cot}\:\mathrm{2x}+\mathrm{cot}\:\mathrm{2xcot}\:\mathrm{3x}=\mathrm{cot}\:\mathrm{x}\left(\mathrm{cot}\:\mathrm{x}−\mathrm{cot}\:\mathrm{3x}\right) \\ $$
