
Question Number 105892 by mohammad17 last updated on 01/Aug/20
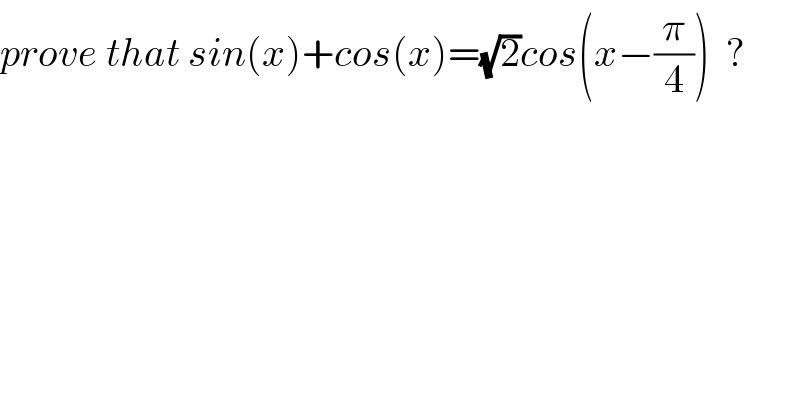
$${prove}\:{that}\:{sin}\left({x}\right)+{cos}\left({x}\right)=\sqrt{\mathrm{2}}{cos}\left({x}−\frac{\pi}{\mathrm{4}}\right)\:\:? \\ $$
Answered by john santu last updated on 01/Aug/20
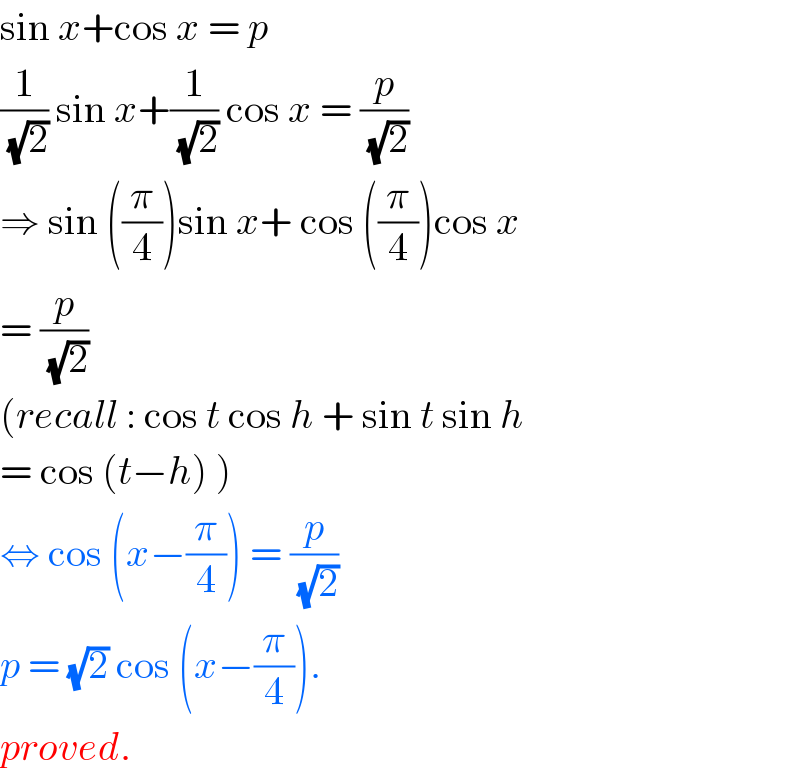
$$\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:=\:{p} \\ $$$$\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\mathrm{sin}\:{x}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\mathrm{cos}\:{x}\:=\:\frac{{p}}{\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}\right)\mathrm{sin}\:{x}+\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}\right)\mathrm{cos}\:{x} \\ $$$$=\:\frac{{p}}{\sqrt{\mathrm{2}}}\:\: \\ $$$$\left({recall}\::\:\mathrm{cos}\:{t}\:\mathrm{cos}\:{h}\:+\:\mathrm{sin}\:{t}\:\mathrm{sin}\:{h}\right. \\ $$$$\left.=\:\mathrm{cos}\:\left({t}−{h}\right)\:\right) \\ $$$$\Leftrightarrow\:\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right)\:=\:\frac{{p}}{\sqrt{\mathrm{2}}} \\ $$$${p}\:=\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left({x}−\frac{\pi}{\mathrm{4}}\right). \\ $$$${proved}. \\ $$
Commented by mohammad17 last updated on 01/Aug/20

$${thank}\:{you}\:{sir} \\ $$
