
Question Number 105764 by bobhans last updated on 31/Jul/20
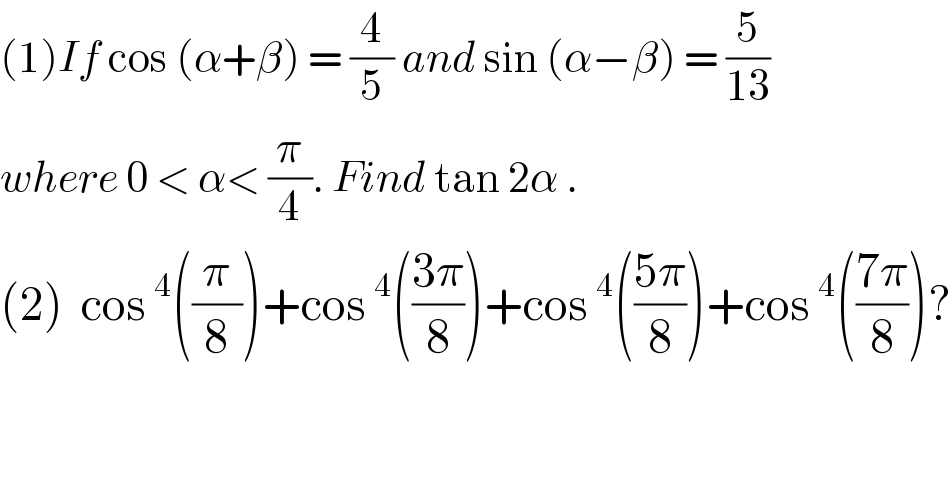
$$\left(\mathrm{1}\right){If}\:\mathrm{cos}\:\left(\alpha+\beta\right)\:=\:\frac{\mathrm{4}}{\mathrm{5}}\:{and}\:\mathrm{sin}\:\left(\alpha−\beta\right)\:=\:\frac{\mathrm{5}}{\mathrm{13}} \\ $$ $${where}\:\mathrm{0}\:<\:\alpha<\:\frac{\pi}{\mathrm{4}}.\:{Find}\:\mathrm{tan}\:\mathrm{2}\alpha\:. \\ $$ $$\left(\mathrm{2}\right)\:\:\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)? \\ $$
Commented byDwaipayan Shikari last updated on 31/Jul/20

$$\left.\mathrm{2}\right)\frac{\mathrm{17}}{\mathrm{16}} \\ $$
Answered by bemath last updated on 01/Aug/20
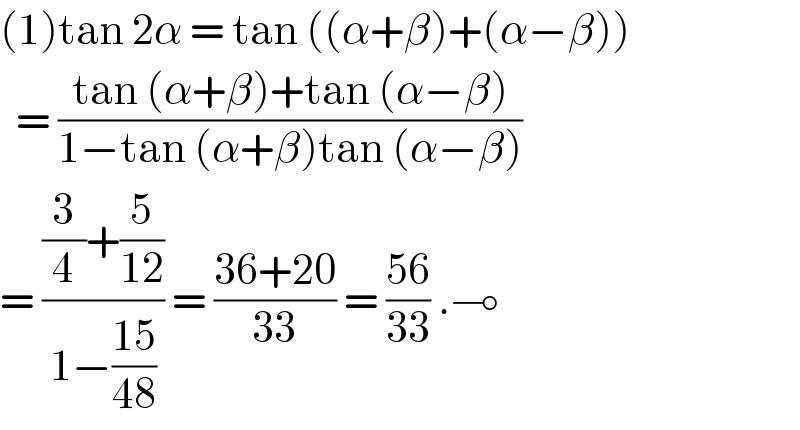
$$\left(\mathrm{1}\right)\mathrm{tan}\:\mathrm{2}\alpha\:=\:\mathrm{tan}\:\left(\left(\alpha+\beta\right)+\left(\alpha−\beta\right)\right) \\ $$ $$\:\:=\:\frac{\mathrm{tan}\:\left(\alpha+\beta\right)+\mathrm{tan}\:\left(\alpha−\beta\right)}{\mathrm{1}−\mathrm{tan}\:\left(\alpha+\beta\right)\mathrm{tan}\:\left(\alpha−\beta\right)} \\ $$ $$=\:\frac{\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{12}}}{\mathrm{1}−\frac{\mathrm{15}}{\mathrm{48}}}\:=\:\frac{\mathrm{36}+\mathrm{20}}{\mathrm{33}}\:=\:\frac{\mathrm{56}}{\mathrm{33}}\:.\multimap \\ $$
Commented byPRITHWISH SEN 2 last updated on 31/Jul/20
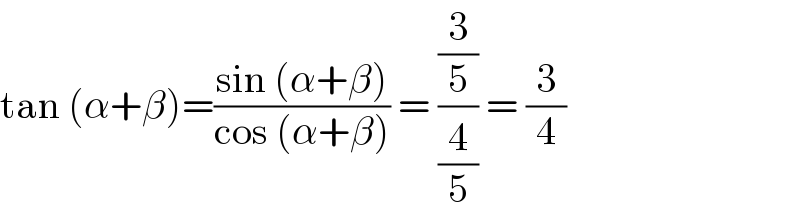
$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\mathrm{cos}\:\left(\alpha+\beta\right)}\:=\:\frac{\frac{\mathrm{3}}{\mathrm{5}}}{\frac{\mathrm{4}}{\mathrm{5}}}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Answered by john santu last updated on 31/Jul/20
![(2)cos (((5π)/8))= cos (((3π)/8)) and cos (((7π)/8))=cos ((π/8)) ⇔ 2{ cos^4 ((π/8))+cos^4 (((3π)/8))} = 2{(cos^2 ((π/8))+cos^2 (((3π)/8)))^2 − 2cos^2 ((π/8))cos^2 (((3π)/8))} ⇔let A= [ cos^2 ((π/8))+cos^2 (((3π)/8)) ]^2 = [(cos (π/8)+cos ((3π)/8))^2 −2 cos (π/8).cos ((3π)/8) ]^2 =](Q105777.png)
$$\left(\mathrm{2}\right)\mathrm{cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)=\:\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:{and}\:\mathrm{cos}\:\left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{8}}\right) \\ $$ $$\Leftrightarrow\:\mathrm{2}\left\{\:\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right\}\:=\:\mathrm{2}\left\{\left(\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right)^{\mathrm{2}} \right. \\ $$ $$\left.−\:\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right\} \\ $$ $$\Leftrightarrow{let}\:{A}=\:\:\left[\:\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:\right]^{\mathrm{2}} =\:\left[\left(\mathrm{cos}\:\frac{\pi}{\mathrm{8}}+\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{2}\right. \\ $$ $$\left.\mathrm{cos}\:\frac{\pi}{\mathrm{8}}.\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{8}}\:\right]\:^{\mathrm{2}} \:=\: \\ $$
Answered by som(math1967) last updated on 01/Aug/20

$$\left.\mathrm{2}\right)\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{5}\pi}{\mathrm{8}}=\mathrm{cos}^{\mathrm{4}} \left(\pi−\frac{\mathrm{3}\pi}{\mathrm{8}}\right)=\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$ $$\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{7}\pi}{\mathrm{8}}=\mathrm{cos}^{\mathrm{4}} \left(\pi−\frac{\pi}{\mathrm{8}}\right)=\mathrm{cos}^{\mathrm{4}} \frac{\pi}{\mathrm{8}} \\ $$ $$\mathrm{cos}^{\mathrm{4}} \frac{\pi}{\mathrm{8}}+\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{8}}+\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{5}\pi}{\mathrm{8}}+\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{7}\pi}{\mathrm{8}} \\ $$ $$\mathrm{2}\left(\mathrm{cos}^{\mathrm{4}} \frac{\pi}{\mathrm{8}}+\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$ $$\mathrm{2}\left(\mathrm{cos}^{\mathrm{4}} \frac{\pi}{\mathrm{8}}\:+\mathrm{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{8}}\right)\:\bigstar \\ $$ $$\left(\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\:+\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\:−\mathrm{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)^{\mathrm{2}} \\ $$ $$=\mathrm{1}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{4}} \\ $$ $$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{ans} \\ $$ $$\bigstar\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)=\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} +\left(\mathrm{a}−\mathrm{b}\right)^{\mathrm{2}} \\ $$ $$\mathrm{cos}^{\mathrm{4}} \frac{\mathrm{3}\pi}{\mathrm{8}}=\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{8}}\right)=\mathrm{sin}^{\mathrm{4}} \frac{\pi}{\mathrm{8}} \\ $$
Commented by1549442205PVT last updated on 01/Aug/20

$$\boldsymbol{\mathrm{There}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{mistake}}\:\boldsymbol{\mathrm{ocurring}}\:\boldsymbol{\mathrm{at}}\:\boldsymbol{\mathrm{fourth}} \\ $$ $$\boldsymbol{\mathrm{line}}\:\boldsymbol{\mathrm{up}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{below}}\:\boldsymbol{\mathrm{cos}}^{\mathrm{4}} \frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{8}}\neq\boldsymbol{\mathrm{sin}}^{\mathrm{4}} \frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{4}}. \\ $$
Commented bybobhans last updated on 01/Aug/20
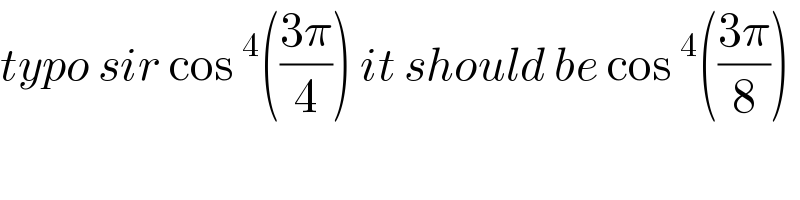
$${typo}\:{sir}\:\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right)\:{it}\:{should}\:{be}\:\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$ $$ \\ $$
Commented bysom(math1967) last updated on 01/Aug/20

$$\mathrm{yes}\:\mathrm{sir}\:\mathrm{I}\:\mathrm{fix}\:\mathrm{it} \\ $$
Answered by mathmax by abdo last updated on 03/Aug/20
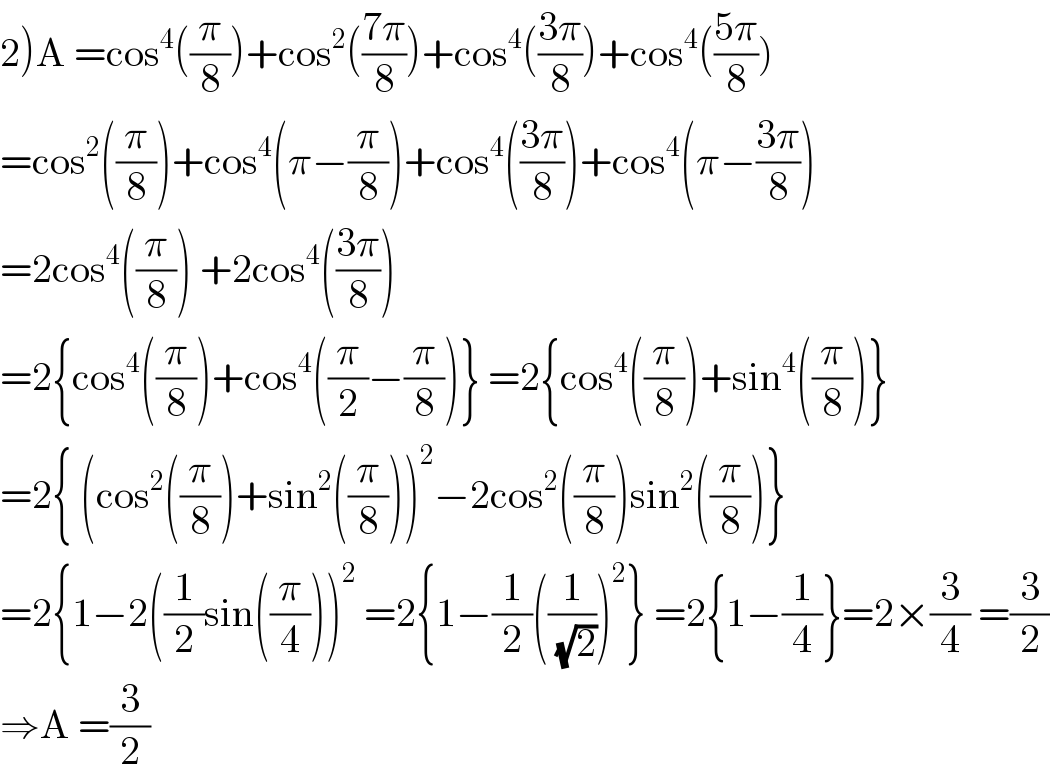
$$\left.\mathrm{2}\right)\mathrm{A}\:=\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{4}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right) \\ $$ $$=\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{4}} \left(\pi−\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{4}} \left(\pi−\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$ $$=\mathrm{2cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)\:+\mathrm{2cos}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$ $$=\mathrm{2}\left\{\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\right)\right\}\:=\mathrm{2}\left\{\mathrm{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{sin}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)\right\} \\ $$ $$=\mathrm{2}\left\{\:\left(\mathrm{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\right)^{\mathrm{2}} −\mathrm{2cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\right\} \\ $$ $$=\mathrm{2}\left\{\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}\right)\right)^{\mathrm{2}} \:=\mathrm{2}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \right\}\:=\mathrm{2}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right\}=\mathrm{2}×\frac{\mathrm{3}}{\mathrm{4}}\:=\frac{\mathrm{3}}{\mathrm{2}}\right. \\ $$ $$\Rightarrow\mathrm{A}\:=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
