
Question Number 105748 by ZiYangLee last updated on 31/Jul/20
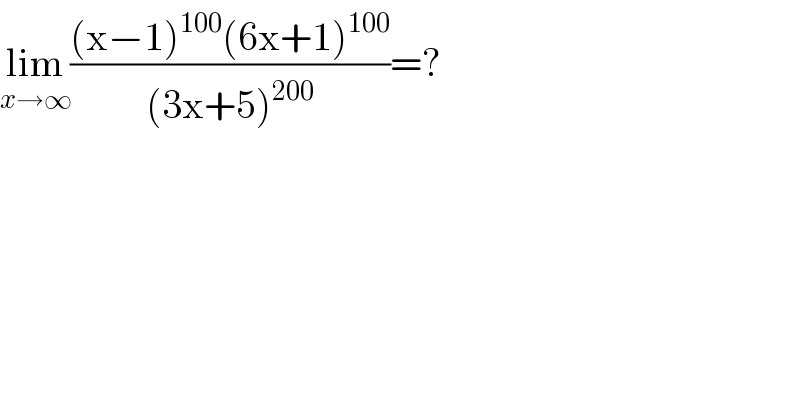
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{100}} \left(\mathrm{6x}+\mathrm{1}\right)^{\mathrm{100}} }{\left(\mathrm{3x}+\mathrm{5}\right)^{\mathrm{200}} }=? \\ $$
Answered by john santu last updated on 31/Jul/20
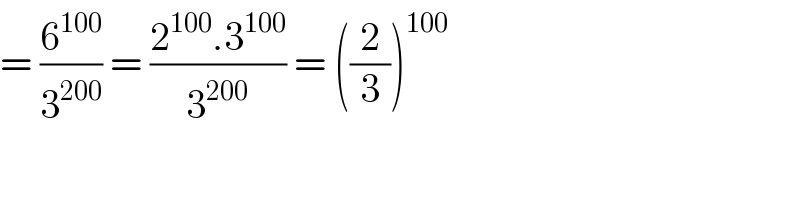
$$=\:\frac{\mathrm{6}^{\mathrm{100}} }{\mathrm{3}^{\mathrm{200}} }\:=\:\frac{\mathrm{2}^{\mathrm{100}} .\mathrm{3}^{\mathrm{100}} }{\mathrm{3}^{\mathrm{200}} }\:=\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{100}} \\ $$
Answered by mathmax by abdo last updated on 31/Jul/20
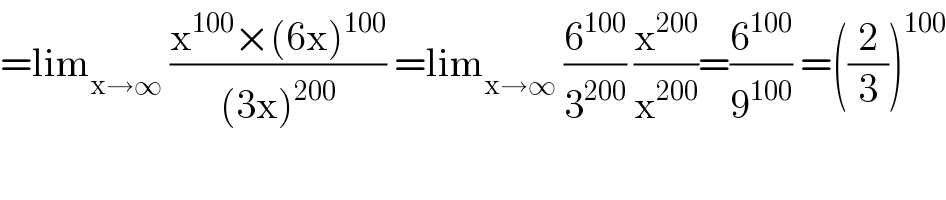
$$=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \:\frac{\mathrm{x}^{\mathrm{100}} ×\left(\mathrm{6x}\right)^{\mathrm{100}} }{\left(\mathrm{3x}\right)^{\mathrm{200}} }\:=\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \:\frac{\mathrm{6}^{\mathrm{100}} }{\mathrm{3}^{\mathrm{200}} }\:\frac{\mathrm{x}^{\mathrm{200}} }{\mathrm{x}^{\mathrm{200}} }=\frac{\mathrm{6}^{\mathrm{100}} }{\mathrm{9}^{\mathrm{100}} }\:=\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{100}} \\ $$
Commented by ZiYangLee last updated on 31/Jul/20

$$\mathrm{thx} \\ $$
